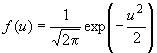ГОСТ Р 50779.10-2000
Статистические методы. Вероятность и основы статистики. Термины и определения

1.1 вероятность

en probability

Действительное число в интервале от 0 до 1, относящееся к случайному событию.

fr

Примечания

1 Число может отражать относительную частоту в серии наблюдений или степень уверенности в том, что некоторое событие произойдет. Для высокой степени уверенности вероятность близка к единице.

2 Вероятность события обозначают или

1.2 случайная величина

en random variable; variate

Переменная, которая может принимать любое значение из заданного множества значений и с которой связано распределение вероятностей.

fr variable

Примечание - Случайную величину, которая может принимать только отдельные значения, называют дискретной. Случайную величину, которая может принимать любые значения из конечного или бесконечного интервала, называют непрерывной

1.3 распределение (вероятностей)

en probability distribution

Функция, определяющая вероятность того, что случайная величина примет какое-либо заданное значение или будет принадлежать заданному множеству значений.

fr loi de

Примечание - Вероятность того, что случайная величина находится в области ее изменения, равна единице

1.4 функция распределения

en distribution function

Функция, задающая для любого значения вероятность того, что случайная величина меньше или равна ,

fr fonction de

1.5 плотность распределения (вероятностей)

en probability density function

Первая производная, если она существует, функции распределения непрерывной случайной величины

fr fonction de de

.

Примечание - называется элементом вероятности

1.6 функция распределения (вероятностей) масс

en probability mass function

Функция, дающая для каждого значения дискретной случайной величины вероятность того, что случайная величина равна :

fr fonction de masse

1.7 двумерная функция распределения

en bivariate distribution function

Функция, дающая для любой пары значений , вероятность того, что случайная величина будет меньше или равна , а случайная величина - меньше или равна :

fr fonction de deux variables

.

Примечание - Выражение в квадратных скобках означает пересечение событий и

1.8 многомерная функция распределения

en multivariate distribution function

Функция, дающая для любого набора значений , ,... вероятность того, что несколько случайных величин , ,... будут меньше или равны соответствующим значениям , ,...:

fr fonction de plusieurs variables

1.9 маргинальное распределение (вероятностей)

en marginal probability distribution

Распределение вероятностей подмножества из множества случайных величин, при этом остальные случайные величины принимают любые значения в соответствующих множествах возможных значений.

fr loi de marginale

Примечание - Для распределения вероятностей трех случайных величин , , существуют:

- три двумерных маргинальных распределения, т.е. распределения пар , , ;

- три одномерных маргинальных распределения, т.е. распределения , и

1.10 условное распределение (вероятностей)

en conditional probability distribution

Распределение подмножества случайных величин из распределения случайных величин, когда остальные случайные величины принимают постоянные значения.

fr loi de conditionnelle

Примечание - Для распределения вероятностей двух случайных величин , существуют:

- условные распределения : некоторое конкретное распределение представляют как "распределение при ";

- условные распределения : некоторое конкретное распределение представляют как "распределение при "

1.11 независимость (случайных величин)

en independence

Две случайные величины и независимы, если их функции распределения представлены как

fr

,

где и - маргинальные функции распределения и , соответственно, для всех пар .

Примечания

1 Для непрерывной независимой случайной величины ее плотность распределения, если она существует, выражают как

,

где и - маргинальные плотности распределения и , соответственно, для всех пар .

Для дискретной независимой случайной величины ее вероятности выражают как

для всех пар .

2 Два события независимы, если вероятность того, что они оба произойдут, равна произведению вероятностей этих двух событий

1.12 параметр

en parameter

Величина, используемая в описании распределения вероятностей некоторой случайной величины

fr

1.13 корреляция

en correlation

Взаимозависимость двух или нескольких случайных величин в распределении двух или нескольких случайных величин.

fr

Примечание - Большинство статистических мер корреляции измеряют только степень линейной зависимости

1.14 квантиль (случайной величины)

en quantile

Значение случайной величины , для которого функция распределения принимает значение или ее значение изменяется скачком от меньшего до превышающего .

fr quantile

Примечания

1 Если значение функции распределения равно во всем интервале между двумя последовательными значениями случайной величины, то любое значение в этом интервале можно рассматривать как -квантиль.

2 Величина будет -квантилем, если

.

3 Для непрерывной величины -квантиль - это то значение переменной, ниже которого лежит -я доля распределения.

4 Процентиль - это квантиль, выраженный в процентах

1.15 медиана

en median

Квантиль порядка

fr

1.16 квартиль

en quartile

Квантиль порядка или

fr quartile

1.17 мода

en mode

Значение случайной величины, при котором функция распределения вероятностей масс или плотность распределения вероятностей имеет максимум.

fr mode

Примечание - Если имеется единственная мода, то распределение вероятностей случайной величины называется унимодальным; если имеется более чем одна мода, оно называется многомодальным, в случае двух мод - бимодальным

1.18 математическое ожидание (случайной величины)

en expectation; expected value; mean

a) Для дискретной случайной величины , принимающей значения с вероятностями , математическое ожидание, если оно существует, определяют формулой

fr ; valeur; moyenne

,

где суммируют все значения , которые может принимать случайная величина .

b) Для непрерывной случайной величины , имеющей плотность , математическое ожидание, если оно существует, определяют формулой

,

где интеграл берут по всему интервалу (интервалам) изменения

1.19 маргинальное математическое ожидание

en marginal expectation

Математическое ожидание маргинального распределения случайной величины

fr marginale

1.20 условное математическое ожидание

en conditional expectation

Математическое ожидание условного распределения случайной величины

fr conditionnelle

1.21 центрированная случайная величина

en centred random variable

Случайная величина, математическое ожидание которой равно нулю.

fr variable

Примечание - Если случайная величина имеет математическое ожидание , то соответствующая центрированная случайная величина равна

1.22 дисперсия (случайной величины)

en variance

Математическое ожидание квадрата центрированной случайной величины

fr variance

1.23 стандартное отклонение (случайной величины)

en standard deviation

Положительный квадратный корень из значения дисперсии

fr

1.24 коэффициент вариации (случайной величины)

en coefficient of variation

Отношение стандартного отклонения к абсолютному значению математического ожидания случайной величины

fr coefficient de variation

1.25 стандартизованная случайная величина

en standardized random variable

Случайная величина, математическое ожидание которой равно нулю, а стандартное отклонение - единице.

fr variable

Примечания

1 Если случайная величина имеет математическое ожидание и стандартное отклонение , то соответствующая стандартизованная случайная величина равна

.

Распределение стандартизованной случайной величины называется стандартным распределением.

2 Понятие стандартизованной случайной величины является частным случаем "приведенной случайной величины", определяемой относительно центрального значения и параметра масштаба, отличных от математического ожидания и стандартного отклонения

1.26 момент* порядка относительно начала отсчета

en moment of order about the origin

Математическое ожидание случайной величины в степени для одномерного распределения

fr moment d'ordre par rapport l origine

.

Примечание - Момент первого порядка - математическое ожидание случайной величины

1.27 момент* порядка относительно

en moment of order about an origin

Математическое ожидание величины в степени для одномерного распределения

fr moment d'ordre partir d' une origine

1.28 центральный момент порядка

en central moment of order

Математическое ожидание центрированной случайной величины для одномерного распределения

fr moment d'ordre

.

Примечание - Центральный момент второго порядка - дисперсия случайной величины

1.29 совместный момент* порядков и относительно начала отсчета

en joint moment of orders and about the origin

Математическое ожидание произведения случайной величины в степени и случайной величины в степени для двумерного распределения

fr moment d'ordres et partir de l' origine

.

Примечание - Совместный момент порядков 1 и 0 - маргинальное математическое ожидание случайной величины .

Совместный момент порядков 0 и 1 - маргинальное математическое ожидание случайной величины

1.30 совместный момент* порядков и относительно точки

en joint moment of orders and about an origin

Математическое ожидание произведения случайной величины в степени q и случайной величины в степени для двумерного распределения:

fr moment d'ordres et partir d'une origine

1.31 совместный центральный момент* порядков и

en jiont central moment of orders and

Математическое ожидание произведения центрированной случайной величины в степени и центрированной случайной величины в степени для двумерного распределения:

fr moment d'ordres et

.

Примечание - Совместный центральный момент порядков 2 и 0 - дисперсия маргинального распределения .

Совместный центральный момент порядков 0 и 2 - дисперсия маргинального распределения

_____________________
* Если при определении моментов значения случайных величин и т.д. заменяют на их абсолютные значения и т. д., то моменты называют "абсолютными моментами".

1.32 ковариация; корреляционный момент

en covariance

Совместный центральный момент порядков 1 и 1:

fr covariance

1.33 коэффициент корреляции

en correlation coefficient

Отношение ковариации двух случайных величин к произведению их стандартных отклонений:

fr coefficient de

.

Примечания

1 Эта величина всегда будет принимать значения от минус 1 до плюс 1, включая крайние значения.

2 Если две случайные величины независимы, коэффициент корреляции между ними равен нулю только в случае двумерного нормального распределения

1.34 кривая регрессии (по )

en regression curve

Для двух случайных величин и кривая, отображающая зависимость условного математического ожидания случайной величины при условии для каждой переменной .

fr courbe de

Примечание - Если кривая регрессии по представляет собой прямую линию, то регрессию называют "простой линейной". В этом случае коэффициент линейной регрессии по - это коэффициент наклона перед в уравнении линии регрессии

1.35 поверхность регрессии ( пo и )

en regression surface

Для трех случайных величин , , поверхность, отображающая зависимость условного математического ожидания случайной величины при условии и для каждой пары переменных .

fr surface de

Примечания

1 Если поверхность регрессии представляет собой плоскость, то регрессию называют "линейной". В этом случае коэффициент линейной регрессии по - это коэффициент перед в уравнении регрессии.

2 Определение можно распространить на число случайных величин более трех

1.36 равномерное распределение; прямоугольное распределение

en uniform distribution; rectangular distribution

a) Распределение вероятностей непрерывной случайной величины, плотность распределения вероятности которой постоянна на конечном интервале и равна нулю вне его.

fr loi uniforme; loi rectangulare

b) Распределение вероятностей дискретной случайной величины такое, что

для .

Примечание - Равномерное распределение дискретной случайной величины имеет равные вероятности для каждого из значений, то есть

для

1.37 нормальное распределение; распределение Лапласа - Гаусса

en normal distribution; Laplace - Gauss distribution

Распределение вероятностей непрерывной случайной величины такое, что плотность распределения вероятностей при принимает действительное значение

fr loi normale; loi de Laplace -Gauss

.

Примечание - - математическое ожидание; - стандартное отклонение нормального распределения

1.38 стандартное нормальное распределение; стандартное распределение Лапласа - Гаусса

en standardized normal distribution; standardized Laplace - Gauss distribution

Распределение вероятностей стандартизованной нормальной случайной величины , плотность распределения которой

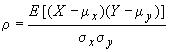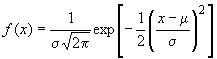fr loi normale ; loi de Laplace - Gauss