ГОСТ Р ИСО 16269-6-2005
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
СТАТИСТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
Определение статистических толерантных интервалов
Statistical methods. Statistical interpretation of data.
Determination of statistical tolerance intervals
ОКС 03.120.30
Дата введения 2005-09-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 ПОДГОТОВЛЕН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции" на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Управлением технического регулирования и стандартизации Федерального агентства по техническому регулированию и метрологии
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 30 июня 2005 г. N 171-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 16269-6:2003 "Статистическое представление данных. Часть 6: Определение статистических толерантных интервалов" (ISO 16269-6:2003 "Statistical interpretation of data-Part 6: Determination of statistical tolerance intervals").
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты, сведения о которых представлены в дополнительном приложении J
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте национального органа Российской Федерации по стандартизации в сети Интернет
Введение
Введение
Толерантный интервал - интервал, определяемый по выборке, относительно которого можно утверждать с уровнем доверия (1-
), что он содержит, по крайней мере, указанную долю 
совокупности. Границы статистического толерантного интервала называются статистическими толерантными границами. Уровень доверия (1-) - вероятность того, что толерантный интервал, определенный описанным методом, будет содержать не менее чем долю совокупности. Наоборот, вероятность того, что толерантный интервал будет содержать менее чем долю совокупности, есть . Настоящий стандарт описывает методы определения односторонних (с верхней или нижней границей) и двусторонних (с верхней и нижней границами) статистических толерантных интервалов.
Толерантный интервал является функцией наблюдений выборки, то есть статистики. Приведенные в настоящем стандарте методы предполагают, что наблюдения в выборке независимы.
В настоящем стандарте приведены два типа методов определения толерантных интервалов: параметрический и непараметрический. Параметрический метод основан на предположении, что исследуемая случайная величина имеет нормальное распределение. Уровень доверия того, что расчетный толерантный интервал содержит не менее чем долю совокупности, составляет (1-), если предположение о нормальности верно. Для определения толерантного интервала используют одну из форм А, В, С и D.
Параметрические методы для распределений, отличных от нормального, в настоящем стандарте не рассмотрены. Если распределение не является нормальным, могут быть применены непараметрические методы. При определении толерантного интервала для любого непрерывного распределения используют формы Е и F.
Рассматриваемые в настоящем стандарте толерантные границы могут быть использованы при статистическом управлении процессом для сравнения возможностей процесса с одним или двумя заданными спецификацией пределами.
Выше верхнего предела 
, установленного спецификацией, имеется доля несоответствий 
, a ниже нижнего предела 
имеется доля несоответствий 
. Сумма 
называется полной долей несоответствий. Между пределами и , установленными спецификацией, имеется доля 1-
.
В статистическом управлении процессом пределы и установлены заранее, а доли , и или рассчитывают, если распределение известно, или оценивают - в противном случае.
Для толерантных интервалов, рассматриваемых в настоящем стандарте, уровень доверия определяемого интервала и доля распределения в границах интервала установлены заранее, а границы оценивают. Эти границы можно сравнивать с и . Следовательно, приемлемость заданных пределов и можно оценить на основе сравнения с фактическими свойствами процесса. Односторонние толерантные интервалы используют, когда спецификацией задана только верхняя граница или только нижняя граница . Двусторонние интервалы используют, когда в спецификации указаны и верхняя и нижняя границы.
Терминология в отношении этих интервалов была очень запутанной, поскольку границы, указанные в спецификации, ранее также называли толерантными границами.
1 Область применения
Настоящий стандарт описывает процедуры определения толерантных интервалов, для которых с заданным уровнем доверия можно утверждать, что они содержат не менее чем заданную долю совокупности. Приведенные методы позволяют определять как односторонние интервалы, имеющие только верхнюю или только нижнюю границу, так и двусторонние интервалы, имеющие и верхнюю и нижнюю границы. В стандарте приведены параметрический метод определения толерантных интервалов для нормального распределения и непараметрический метод. Непараметрический метод определения толерантных интервалов не требует знания вида функции распределения, но применим лишь в случаях, когда известно, что функция распределения совокупности непрерывна.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 2854:1976 Статистическое представление данных. Методы оценки и проверки гипотез о средних значениях и дисперсиях
ИСО 3534.1:1993 Статистика. Словарь и условные обозначения. Часть 1: Вероятность и основы статистики
ИСО 5479:1997 Статистическое представление данных. Критерии отклонения от нормального распределения
3 Термины, определения и обозначения
3.1 В настоящем стандарте применены термины по ИСО 3534.1, а также следующие термины с соответствующими определениями:
3.1.1 толерантный интервал (tolerance interval): Интервал, определенный по случайной выборке таким способом, что можно утверждать с указанным уровнем доверия, что интервал содержит не менее чем заданную долю совокупности.
Примечание - Уровень доверия в этом случае - предел доли интервалов, определенных указанным способом, которые будут включать в себя не менее чем заданную долю совокупности, при бесконечном увеличении повторений метода.
3.1.2 толерантная граница (tolerance limit): Граница толерантного интервала.
Примечание - Статистический толерантный интервал может быть или односторонний, когда он имеет или верхнюю или нижнюю толерантную границу, или двусторонний, когда он имеет обе толерантные границы.
3.2 В настоящем стандарте применены следующие обозначения:
- индекс наблюдения;
- коэффициент, используемый при определении 
или 
для одностороннего толерантного интервала, когда значение 
известно;
- коэффициент, используемый при определении и для двустороннего толерантного интервала, когда значение известно;
- коэффициент, используемый при определении или для одностороннего толерантного интервала, когда значение неизвестно;
- коэффициент, используемый при определении и для двустороннего толерантного интервала, когда значение неизвестно;
- число наблюдений в выборке;
- минимальная доля совокупности, относительно которой утверждают, что она находится внутри толерантного интервала;
- выборочное стандартное отклонение;
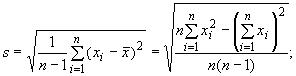
- квантиль стандартного нормального распределения уровня ;
- -e наблюдаемое значение 
;
- максимальная из наблюдаемых величин: 
;
- минимальная из наблюдаемых величин: 
;
- нижняя граница толерантного интервала;
- верхняя граница толерантного интервала;
- выборочное среднее арифметическое значение: 
;
- уровень доверия утверждения, что доля совокупности, находящаяся внутри границ толерантного интервала, больше указанного значения или равна ему;
- среднее совокупности;
- стандартное отклонение совокупности.
4 Процедуры
4.1 Нормальная совокупность с известной дисперсией и известным средним
Когда значения среднего и дисперсии 
нормальной совокупности известны, распределение исследуемой характеристики полностью определено. В этом случае можно определить интервал, содержащий точно долю совокупности:
a) Односторонний интервал с нижней границей 
.
b) Односторонний интервал с верхней границей 
.
c) Двусторонний интервал с нижней границей 
и верхней границей 
.
Примечание - Эти утверждения являются истинными, они соответствуют уровню доверия 100%.
В вышеупомянутых выражениях - квантиль стандартного нормального распределения уровня . Значения приведены в таблицах А.1-А.6 и В.1-В.6.
4.2 Нормальная совокупность с известной дисперсией и неизвестным средним
В том случае, когда дисперсия нормальной совокупности известна, а среднее неизвестно, для определения границ толерантного интервала используют формы А и В. Форму А применяют для определения границ одностороннего интервала, а форму В - для определения границ двустороннего интервала.
4.3 Нормальная совокупность с неизвестной дисперсией и неизвестным средним
В случае, когда и среднее и дисперсия нормальной совокупности неизвестны, применяют формы С и D. Форму С применяют для определения границ одностороннего интервала, а форму D - для определения границ двустороннего интервала.
4.4 Непрерывное распределение неизвестного вида
Если исследуемая характеристика принадлежит совокупности с непрерывной функцией распределения неизвестной формы, то статистический толерантный интервал может быть определен по выборке из независимых случайных наблюдений. Процедура, приведенная в формах Е и F, обеспечивает определение доли совокупности или объема выборки , необходимых для оценки границ толерантных интервалов с критическими значениями выборки или и с уровнем доверия (1-).
Примечание 1 - Статистические толерантные интервалы, которые не зависят от формы функции распределения выбранной совокупности, называются непараметрическими толерантными интервалами.
Настоящий стандарт не содержит процедур оценки границ толерантного интервала для распределений, отличных от нормального распределения. Однако если распределение непрерывно, может быть использован непараметрический метод.
5 Примеры
5.1 Данные
В качестве примеров заполнения форм от А до D использованы числовые данные примера испытаний пряжи из ИСО 2854. Результаты измерений следующие:
|
| 228,6 | 232,7 | 238,8 | 317,2 | 315,8 | 275,1 | 222,2 | 236,7 | 224,7 | 251,2 | 210,4 | 270,7 |
Результаты измерений и вычислений в примерах выражены в сотых долях ньютона. Результаты измерений получены из партии в 12000 катушек, упакованной по 100 катушек. 12 упаковок были наугад выбраны из партии, и из каждой упаковки была вынута наугад одна катушка. Образцы длиной 50 см были вырезаны из пряжи катушек приблизительно на расстоянии 5 м от свободного конца. Испытания на разрыв проводили на центральных частях этих образцов. Данная информация позволяет предположить, что усилия разрыва пряжи, измеренные в этих условиях, имеют нормальное распределение.
Результаты испытаний:
Объем выборки: 
12.
Выборочное среднее арифметическое: =3024,1/12=252,01.
Выборочное стандартное отклонение:
.
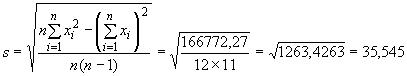Формальное представление вычислений дано только для формы С (односторонний интервал, неизвестная дисперсия).
5.2 Пример 1: Односторонний статистический толерантный интервал при известной дисперсии
Предварительные измерения показали, что дисперсия является постоянной для всех партий одного и того же поставщика и представлена стандартным отклонением 
33,150, хотя среднее партий не является константой. Граница должна быть такой, чтобы можно было утверждать с уровнем доверия (1-)=0,95 (95%), что по крайней мере у 0,95 (95%) единиц партии усилие разрыва больше , если измерения были проведены при одних и тех же условиях.
В соответствии с таблицей А.4:
.
Таким образом,
.
Очевидно, что большей доле совокупности (например, 
0,99 и/или более высокому уровню доверия [например, (1-)=0,99] соответствует меньшее значение границы .
5.3 Пример 2: Двусторонний статистический толерантный интервал при известной дисперсии
В условиях примера 1 необходимо определить такие границы и , для которых можно утверждать с уровнем доверия (1-)=0,95, что по крайней мере для доли 0,90 (90%) единиц партии усилие разрыва попадает между границами и .
В соответствии с таблицей В.4:
.
Таким образом,
;
.
Примечание - Сравнение с примером 1 показывает: уверенность в том, что по крайней мере 90% совокупности лежит между границами и , не отличается от уверенности в том, что не более чем 5% совокупности находится вне каждой границы.
5.4 Пример 3: Односторонний статистический толерантный интервал при неизвестной дисперсии
Стандартное отклонение совокупности неизвестно и должно быть оценено по выборке. Остальные данные - те же, что и в примере 1. Таким образом, 0,95 и (1-)=0,95. Результаты расчетов приведены ниже.
| Определение статистического толерантного интервала для доли |
| Вычисления: |
| Результаты: |
.
;
;
.
.
5.5 Пример 4: Двусторонний статистический толерантный интервал при неизвестной дисперсии
В условиях примера 2 необходимо определить такие границы и , для которых можно утверждать с уровнем доверия (1-)=0,95, что не менее чем доля 0,90 (90%) единиц партии имеет усилие разрыва между и .
В соответствии с таблицей D.4:
.
Таким образом,
;
.
Легко заметить, что значение меньше, а значение больше, чем соответствующие значения в примере 2 (известная дисперсия), поскольку использование вместо вносит дополнительную неопределенность. Расширение статистического толерантного интервала это учитывает. В случае недостаточной уверенности, что значение 
33,150, используемое в примерах 1 и 2, указано правильно, полезно использовать оценку вместе с таблицей С.4 или D.4.
5.6 Пример 5: Непрерывное распределение неизвестного вида
Проведены испытания на усталость одного из компонентов аэронавигационного двигателя. Испытано 15 элементов. Результаты измерений приведены в порядке возрастания:
|
| 0,200 | 0,330 | 0,450 | 0,490 | 0,780 | 0,920 | 0,950 | 0,970 | 1,040 | 1,710 | 2,220 | 2,275 | 3,650 | 7,000 | 8,800 |
Графическая проверка нормальности показывает, что гипотеза о нормальности распределения должна быть отклонена (см. ИСО 5479). Поэтому методы форм С и D для определения статистического толерантного интервала не подходят.
Критические значения для выборки из 15 измерений:
0,200, 
8,800.
Требуемый уровень доверия (1-)=0,95.
a) Какую максимальную долю совокупности составляют элементы, меньшие 
0,200? Таблица Е.1 для (1-)=0,95 дает для минимальной доли элементов, для которых 
, значение чуть выше 0,75 (75%). Следовательно, для максимальной доли элементов, для которых 
, значение 1- чуть ниже 0,25 (25%).
b) Какой объем выборки необходим для того, чтобы можно было утверждать с уровнем доверия 0,95, что по крайней мере доля 0,90 (90%) совокупности будет меньше самого большого значения в выборке? Таблица Е.1 для (1-)=0,95 и 0,90 дает 29.
c) Какую минимальную долю совокупности составляют элементы, для которых 
, для уровня доверия 0,95
0,200 и 
8,800? Таблица F.1 для (1-)=0,95 и 15 дает чуть ниже 0,75 (75%).
d) Какой объем выборки необходим для того, чтобы можно было утверждать с уровнем доверия 0,95, что по крайней мере доля 0,90 (90%) совокупности будет располагаться между самым малым и самым большим значениями в выборке? Таблица F.1 для (1-)=0,95 и 0,90 дает 46.
e) Если проверка нормальности (см. ИСО 5479) указывает на отклонение от нормального распределения, в некоторых случаях можно выполнить преобразование исходных данных, приводящее их к нормальному распределению. Например, данные испытаний на усталость обычно описываются логарифмически нормальным распределением. В этом случае исходные данные легко привести к нормальному распределению. Изложенные методы следует применять к преобразованным нормально распределенным данным. А затем к результатам применяют обратное преобразование.
В приложении G приведены методы построения непараметрических статистических толерантных интервалов, справедливые для любых непрерывных распределений. В приложении Н приведено обоснование расчета коэффициентов для двусторонних статистических толерантных интервалов.
Форма А - Односторонний статистический толерантный интервал (известная дисперсия)
| Определение одностороннего статистического толерантного интервала с долей совокупности |
| Результаты: |
Форма В - Двусторонний статистический толерантный интервал (известная дисперсия)
| Определение двустороннего статистического толерантного интервала с долей |
| Вычисления: |
| Результаты: |
Форма С - Односторонний статистический толерантный интервал (неизвестная дисперсия)
| Определение одностороннего статистического толерантного интервала с долей |
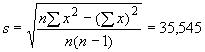