ГОСТ Р 8.580-2001
Группа Т80
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
Определение и применение показателей прецизионности методов испытаний нефтепродуктов
State system for ensuring the uniformity of measurements. Determination and application of precision data in relation to petroleum products tests methods
ОКС 17.020
ОКСТУ 0008
Дата введения 2002-01-01
Предисловие
1 РАЗРАБОТАН Всероссийским научно-исследовательским институтом по переработке нефти (ОАО "ВНИИ НП"), Уральским научно-исследовательским институтом метрологии (УНИИМ)
ВНЕСЕН Управлением метрологии Госстандарта России
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 7 июля 2001 г. N 224-ст
3 Стандарт разработан на основе международного стандарта ИСО 4259-92 "Petroleum Products. Determination and application of precision data in relation to methods of test", который распространяется на определение и применение показателей прецизионности (повторяемости и воспроизводимости) методов испытаний нефти и нефтепродуктов. Показатели прецизионности зависят только от случайных факторов и не связаны с истинным или условно истинным значением (см. 3.14 ИСО 3534-1, ИСО 5725-1)
4 ВВЕДЕН ВПЕРВЫЕ
5 ИЗДАНИЕ (сентябрь 2005 г.) с Изменением N 1, принятым в сентябре 2002 г. (ИУС 12-2002), Поправкой (ИУС 6-2002)
Введение
Свойства товарных нефти и нефтепродуктов оценивают с помощью стандартных лабораторных методов испытаний для контроля качества и проверки соответствия требованиям спецификаций. Два или более измерений одного и того же свойства определенного образца, выполненные каким-либо методом испытаний, обычно не дают точно один и тот же результат. Поэтому необходимо принять статистически обоснованные оценки показателей прецизионности методов введением объективной меры согласованности, которую ожидают для двух или более результатов, полученных в точно определенных условиях.
Пояснения к некоторым понятиям, используемым в настоящем стандарте, приведены в приложении Л.
1 Область применения
1 Область применения
Настоящий стандарт устанавливает способ определения и применение показателей прецизионности [повторяемости (сходимости) и воспроизводимости]* методов испытаний нефти и нефтепродуктов (далее - нефтепродуктов).
________________
* См. приложение Л.
Стандарт не распространяется на материалы и вещества неоднородного состава.
Раздел 1 (Измененная редакция, Изм. N 1).
1а Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
Раздел 1а. (Введен дополнительно, Изм. N 1).
2 Определения
В настоящем стандарте применяют следующие термины с соответствующими определениями. Отдельные определения даны в соответствии с ГОСТ Р ИСО 5725-1, [1] и [2].
(Измененная редакция, Изм. N 1).
2.1 дисперсионный анализ: Метод анализа, позволяющий разложить общую дисперсию результатов испытаний, присущую данному методу, на составляющие, обусловленные действием определенных факторов.
2.2 межлабораторная (лабораторная) дисперсия: Рассеяние результатов, полученных более чем в одной лаборатории, которое обычно больше, чем в случае проведения того же числа испытаний в одной лаборатории.
Примечание - Термин используют при классификации представительных параметров дисперсии генеральной совокупности результатов, например, "лабораторная дисперсия".
2.3 смещение (отклонение): Разность, между математическим ожиданием результатов испытаний и известным значением, если его можно определить.
Примечания
1 Для целей данного стандарта математическое ожидание (среднее значение заданной совокупности результатов испытаний) выполняет роль "истинного значения или опорного значения" (см. 2.24) (ГОСТ Р ИСО 5725-1, 3.5, d).
Для целей данного стандарта "известное значение" по 2.8.
(Измененная редакция, Изм. N 1).
2.4 кодирование проб: Присвоение различным пробам определенных неповторяющихся номеров, при этом оператор не должен иметь другой идентификации или информации о пробах.
2.5 контрольная проба (проба для испытания): Проба, отобранная в месте передачи продукта, т.е. в месте, где ответственность за качество продукта переходит от поставщика к получателю.
2.6 число степеней свободы: Делитель, используемый в расчете дисперсии (число, которое на единицу меньше числа независимых результатов).
Примечание - Данное определение применимо только к простейшим случаям. Исчерпывающие определения выходят за область данного стандарта.
2.7 определение: Процесс выполнения серии операций, регламентированных в документе на метод испытаний, в результате выполнения которых получают единичное значение.
2.8 известное значение: Действительное количественное значение величины, установленное процедурой приготовления.
Примечание - Известное значение существует не всегда. Оно не может быть определено для эмпирических условных величин (например, температуры вспышки).
2.9 среднее значение (среднеарифметическое значение, среднее): Сумма результатов для данного ряда, деленная на их число.
2.10 средний квадрат: Сумма квадратов, деленная на число степеней свободы.
2.11 нормальное распределение: Распределение вероятностей случайной непрерывной величины , если
- любое действительное число, при котором плотность вероятности составляет
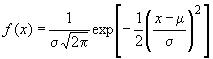 , (1)
, (1)
![]() ,
,
где - истинное значение,
- среднеквадратическое отклонение для нормального распределения (
> 0).
2.12 оператор: Лицо, выполняющее операции испытаний.
2.13 выброс: Элемент совокупности значений, который несовместим с остальными элементами данной совокупности (см. ГОСТ Р ИСО 5725-1).
Примечание - Статистические критерии (меры и уровни значимости), используемые для идентификации выбросов в экспериментах по оценке прецизионности на основе исследований результатов межлабораторных испытаний, изложены в разделе 4 настоящего стандарта.
2.14 прецизионность: Степень близости друг к другу независимых результатов испытаний, полученных в конкретных регламентированных условиях (см. ГОСТ Р ИСО 5725-1 и [2]).
Примечание - "Независимые результаты испытаний" - результаты, полученные способом, на который не оказывает влияния никакой предшествующий результат, полученный при испытаниях того же самого или подобного объекта. Количественные значения мер прецизионности существенно зависят от регламентированных условий. Крайними случаями таких условий являются условия повторяемости и условия воспроизводимости [2].
2.13, 2.14 (Измененная редакция, Изм. N 1).
2.15 (Исключен, Изм. N 1).
2.16 получатель: Лицо или организация, которые получают или принимают поставляемый поставщиком продукт.
2.17 Повторяемость (сходимость) метода
2.17.1 повторяемость результатов испытаний: Степень близости друг к другу независимых результатов испытаний, полученных одним и тем же методом на идентичном материале, в одной и той же лаборатории, одним и тем же оператором, с использованием одного и того же оборудования в пределах короткого промежутка времени [2].
Примечание - Вероятностными характеристиками (статистическими оценками), показателями повторяемости результатов испытаний являются среднеквадратическое отклонение результатов испытаний в условиях повторяемости, дисперсия в условиях повторяемости. Термин "повторяемость (сходимость) результатов испытаний" не следует смешивать с термином "повторное испытание" (в 2.18). Повторяемость (сходимость) относят к состоянию, когда случайная изменчивость результатов минимальна. Поэтому период времени, в течение которого получают повторные результаты, должен быть минимальным, чтобы исключить ошибки, зависящие от времени, например ошибки, связанные с влиянием окружающей среды и стабильностью градуировки.
2.17.2 предел повторяемости (сходимости) : Абсолютное значение разности двух единичных результатов испытаний, полученных в условиях повторяемости (см. 2.17.1) с доверительной вероятностью 95%.
2.18 повторное испытание: Многократное выполнение испытаний с соблюдением требований методики с целью повышения прецизионности результатов испытаний и получения меньшей ошибки испытаний. Повторное испытание следует отличать от обычного повторения, так как оно предполагает выполнение повторных испытаний (дублей) в одном месте и, по возможности, в одно и то же время. Повторным испытанием качественно определяют представительные характеристики дисперсии генеральной совокупности, которые могут быть связаны с повторными экспериментами при повторном испытании, например среднеквадратическое отклонение результатов для повторных испытаний.
2.17.1-2.18 (Измененная редакция, Изм. N 1).
2.19 Воспроизводимость метода
2.19.1 воспроизводимость результатов испытаний: Степень близости друг к другу независимых результатов испытаний, полученных одним и тем же методом на идентичном материале в разных лабораториях, разными операторами, с использованием различного оборудования [3].
Примечание - Вероятностными характеристиками (статистическими оценками), показателями воспроизводимости результатов испытаний являются среднеквадратическое отклонение результатов испытаний в условиях воспроизводимости, дисперсия в условиях воспроизводимости.
2.19.2 предел воспроизводимости : Абсолютное значение разности двух результатов испытаний в условиях воспроизводимости (см. 2.19.1) с доверительной вероятностью 95%.
2.19.1, 2.19.2. (Измененная редакция, Изм. N 1).
2.20 результат испытаний: Значение, полученное на одном или нескольких определениях в зависимости от требований, регламентированных в документе на метод испытаний (результат округляют в соответствии с приложением Ж).
2.21 среднеквадратическое отклонение: Мера рассеяния серий результатов испытаний относительно среднего значения равна положительному значению квадратного корня из дисперсии (оценивают по положительному значению квадратного корня из среднего квадрата).
2.22 сумма квадратов: Сумма квадратов разностей серий результатов и их среднего значения.
2.23 поставщик: Лицо или организация, которые отвечают за качество продукта вплоть до того момента, когда продукт принят получателем.
2.24 принятое опорное значение (для целей данного стандарта выполняет роль истинного значения): Значение, которое служит в качестве согласованного для сравнения с результатом испытаний и получено как математическое ожидание измеряемой характеристики, то есть среднее значение заданной совокупности результатов испытаний, полученных в лабораториях при условии, что
неограниченно возрастает (стремится к бесконечности). Истинное значение (принятое опорное значение) зависит от применяемого метода испытаний [2].
(Измененная редакция, Изм. N 1).
2.25 дисперсия: Среднее значение квадратов отклонения случайной переменной от ее среднего, которое оценивают по среднему квадрату.
3 Программа межлабораторных испытаний для определения показателей прецизионности метода испытаний
3.1 Планирование программы межлабораторных испытаний
3.1.1 Планирование программы межлабораторных испытаний состоит из следующих этапов:
а) подготовка проекта документа на метод испытаний;
б) планирование программы пилотных испытаний с участием двух или более лабораторий;
в) планирование программы межлабораторных испытаний.
3.1.2 Подготовка проекта документа на метод испытаний
Документ должен содержать описание всех необходимых деталей выполнения испытаний и форму отчета о результатах испытания. Любое условие, которое может повлиять на результаты, должно быть регламентировано.
Раздел, относящийся к показателям прецизионности, следует включать на этой стадии только в виде заглавия раздела.
3.1.3 Планирование программы пилотных испытаний с участием двух или более лабораторий
3.1.3.1 Программа пилотных испытаний необходима для:
а) детальной проверки операций испытаний;
б) выяснения возможности успешного выполнения оператором инструкций в документе на метод испытаний;
в) контроля мер предосторожности при обращении с пробами;
г) предварительной оценки показателей прецизионности результатов испытаний.
3.1.3.2 Для того, чтобы охватить диапазон определяемых значений результатов испытаний указанного метода, используют не менее двух проб. Следует включать не менее 12 комбинаций "лаборатория х проба". Каждую пробу испытывают дважды в каждой лаборатории в условиях повторяемости (сходимости). Если в проекте документа на метод выявляют какие-либо упущения или неточности, на этом этапе их следует исправить. Результаты следует анализировать с точки зрения их повторяемости (сходимости), воспроизводимости и наличия смещения. Если нарушение одного из этих условий слишком велико, следует рассмотреть необходимые изменения метода испытаний.
3.1.4 Планирование программы межлабораторных испытаний
3.1.4.1 Необходимо, чтобы в испытаниях участвовало пять или более лабораторий. Для уменьшения требуемого количества проб в испытаниях должны участвовать не менее шести лабораторий.
Количество проб должно быть достаточным, чтобы охватить диапазон уровней измеряемого свойства и обеспечить надежность оценок показателей прецизионности. Если результаты пилотных испытаний обнаруживают какое-либо изменение показателей прецизионности в зависимости от уровня свойства, тогда в программе межлабораторных испытаний следует предусмотреть использование не менее пяти проб. В любом случае необходимо получить не менее 30 степеней свободы и для повторяемости (сходимости), и для воспроизводимости метода. Это означает, что при планировании программы следует добиваться того, чтобы для повторяемости (сходимости) общее число пар результатов было не менее 30.
3.1.4.2 Что касается воспроизводимости, то в приложении А минимальное число необходимых для испытаний проб приведено в зависимости от общего числа лабораторий - участников испытаний (), отношений оценок составляющих (компонент) дисперсии (
), полученных в результате выполнения пилотной программы. При этом
представляет отношение компоненты, обусловленной взаимодействием, к компоненте по дублям, а
- отношение лабораторной компоненты к компоненте по дублям.
В приложении Б приведены формулы, использованные при составлении таблицы А.1. Если много больше, чем
, то невозможно получить 30 степеней свободы для дисперсии. Пропуски в таблице А.1 соответствуют этой или близкой к этой ситуациям (т.е. случаям, когда для испытаний необходимо более 20 проб). В этих случаях вероятны существенные расхождения между лабораториями.
3.2 Выполнение программы межлабораторных испытаний
3.2.1 За выполнение всей программы испытаний, начиная с распространения документов и проб и кончая оцениванием результатов испытаний, должно быть ответственным одно лицо. Это лицо должно быть знакомо с методом испытаний, однако ему не следует лично принимать участие в испытаниях.
Документ с описанием метода должен быть передан всем лабораториям заблаговременно. Если какой-либо лаборатории необходимо получить опыт выполнения операций метода заранее, то эту работу следует выполнять на других пробах, а не на тех, которые используют в рамках программы.
3.2.2 Пробы должны быть складированы, разделены на части, закодированы и распределены организатором испытаний, которому следует хранить резервное количество проб на случай непредвиденных обстоятельств. При этом важно, чтобы порции для отдельных лабораторий оставались однородными.
При рассылке пробы должны быть снабжены следующими документами и инструкциями:
а) согласованный проект документа на метод испытаний;
б) инструкции по хранению проб и обращению с ними;
в) порядок, в котором пробы необходимо испытывать (для каждой лаборатории случайный порядок различен);
г) указание о том, что два результата должны быть получены на одной пробе последовательно одним оператором на одном комплекте оборудования. По статистическим причинам важно, чтобы два результата были получены независимо один от другого, т.е. чтобы знание первого результата не вызывало смещение второго результата. При невозможности исключения субъективности оператора необходимо получать пары результатов в режиме слепого кодирования, но таким образом, чтобы обеспечить выполнение испытаний в короткий интервал времени;
д) период времени, в течение которого должны быть получены повторные результаты испытаний, и период времени, в течение которого должны быть испытаны все пробы;
е) форма протокола для отчета о результатах испытаний. Для каждой пробы должно быть предусмотрено место для даты проведения испытаний, двух результатов и комментариев по любым необычным обстоятельствам. Специально следует указать число значащих цифр в отчете о результатах испытаний;
ж) указание о том, что испытания должны быть выполнены в обычных условиях проведения испытаний с привлечением опытных операторов и продолжительность испытаний должна быть такой же, как при обычных испытаниях.
Операторы, принимавшие участие в выполнении пилотной программы испытаний, могут принимать участие и в выполнении программы межлабораторных испытаний. Если их дополнительный опыт в проведении испытаний небольшого дополнительного числа проб оказывает заметное влияние, то это должно служить предупреждением о том, что исследуемый метод является неудовлетворительным. Для того, чтобы любой такой эффект можно было обнаружить, необходимо в отчете о результатах испытаний обеспечить возможность идентификации этих операторов.
4 Исследование результатов межлабораторных испытаний с целью проверки однородности и выявления выбросов
По результатам выполнения статистически обоснованной программы межлабораторных испытаний (раздел 3) устанавливают:
а) зависимость или независимость показателей прецизионности от уровня результатов испытаний;
б) однородность показателей прецизионности для всех лабораторий и присутствие выбросов (аномальных результатов).
Технические приемы расчета результатов испытаний и примеры (расчет бромного числа) в обозначениях, указанных в приложении В, приведены в приложении Г.
Предполагают, что все результаты получены из одной нормально распределенной совокупности, либо существует возможность их преобразования в такую совокупность (4.1). Другие случаи требуют иной обработки, которая выходит за сферу действия этого стандарта [10].
Несмотря на то, что приведенные технические приемы представлены в форме, приспособленной для расчета вручную, рекомендуется использовать электронный компьютер для хранения и анализа результатов межлабораторных испытаний.
4.1 Преобразование данных
4.1.1 Для многих методов испытаний наблюдается зависимость показателей прецизионности от уровня результатов испытаний, поэтому изменчивость сообщенных результатов различается при переходе от пробы к пробе. Такое положение исправляют с помощью преобразования данных.
4.1.2 Рассчитывают лабораторные среднеквадратические отклонения и среднеквадратические отклонения для дублей
(приложение В) и строят графики зависимости их от средних значений по пробе
. Если через точки, нанесенные на графике, можно провести две линии, параллельные оси значений
, тогда нет необходимости вводить преобразование.
Если через точки, нанесенные на графике, можно построить прямые непараллельные оси значений или кривые, построенные по этим точкам, могут быть описаны зависимостями
![]() и
и ![]() ,
,
то необходимо вводить преобразование.
4.1.3 Зависимости ![]() и
и ![]() в общем случае не будут идентичны. Однако статистические процедуры этого стандарта требуют, чтобы и для повторяемости (сходимости), и для воспроизводимости было применено одно и то же преобразование. Обе зависимости комбинируют в единую зависимость в форме
в общем случае не будут идентичны. Однако статистические процедуры этого стандарта требуют, чтобы и для повторяемости (сходимости), и для воспроизводимости было применено одно и то же преобразование. Обе зависимости комбинируют в единую зависимость в форме ![]() , включающей фиктивную переменную
, включающей фиктивную переменную , причем
теперь включает и
. Эта процедура учитывает различие между двумя зависимостями, если оно существует, и обеспечивает возможность выявления этого различия.
В приложении Д приведены виды зависимостей и подходящие преобразования.
Единую зависимость ![]() оценивают с помощью метода взвешенного линейного регрессионного анализа (приложение Е). Следует использовать взвешенную регрессию с итерациями, однако в большинстве случаев даже простая регрессия будет давать удовлетворительную аппроксимацию. Вывод весовых функций изложен в Е.2, а расчетная процедура для регрессионного анализа - в Е.З. Типичные формы зависимости
оценивают с помощью метода взвешенного линейного регрессионного анализа (приложение Е). Следует использовать взвешенную регрессию с итерациями, однако в большинстве случаев даже простая регрессия будет давать удовлетворительную аппроксимацию. Вывод весовых функций изложен в Е.2, а расчетная процедура для регрессионного анализа - в Е.З. Типичные формы зависимости ![]() даны в Д.1. Все они выражены в терминах параметра единого преобразования
даны в Д.1. Все они выражены в терминах параметра единого преобразования .
4.1.4 Оценивание и следующая за этим процедура преобразования суммированы в Д.1. Это включает статистические испытания значимости регрессии (т.е. является ли зависимость
![]() параллельной оси значений
параллельной оси значений ) и значимости различия между зависимостями для повторяемости (сходимости) и воспроизводимости. Решения по испытаниям принимают на основе 5%-ного уровня значимости. Если обнаружено, что различие между зависимостями существует или отсутствует подходящее преобразование, следует использовать альтернативные методы [1]. В этом случае невозможно проводить испытание с целью выявления систематического смещения лаборатории по всем пробам по 4.5 либо отдельно оценивать компоненту дисперсии по взаимодействию в соответствии с 5.1.
4.1.5 Если на 5%-ном уровне значимости было показано, что значимая регрессия в форме ![]() существует, тогда соответствующее преобразование
существует, тогда соответствующее преобразование ![]() , где
, где - сообщенный результат, выражают формулой
![]() , (2)
, (2)
где - постоянная величина.
В этом случае все результаты следует соответствующим образом преобразовать и последующую часть анализа выполнять в терминах преобразованных результатов (Д.1).
При выборе преобразования в конкретных случаях может потребоваться помощь квалифицированного статистика. На правильность решения о выборе типа преобразования по 4.6 могут влиять аномальные результаты.
Пример - В таблице 1 представлены значения и
с тремя значащими цифрами для восьми проб из приведенного в приложении Г примера. Соответствующие степени свободы приведены в скобках.
Таблица 1
| Параметр | Значение для пробы | |||||||
| 3 | 8 | 1 | 4 | 5 | 6 | 2 | 7 | |
| | 0,756 | 1,22 | 2,15 | 3,64 | 10,9 | 48,2 | 65,4 | 114 |
| | 0,0669 (14) | 0,159 | 0,729 | 0,211 (11) | 0,291 | 1,50 | 2,22 | 2,93 |
| | 0,0500 (9) | 0,0572 (9) | 0,127 | 0,116 | 0,0943 | 0,527 | 0,818 | 0,935 |
и
возрастают с ростом
, причем скорость возрастания падает по мере увеличения
. График зависимости этих величин в билогарифмических координатах (т.е. график зависимости
![]() и
и от
![]() ) показывает, что вполне допустимо рассматривать эти точки как лежащие на двух прямых линиях (рисунок Е.1). Расчеты, приведенные в Е.4, показывают, что градиенты этих линий одни и те же и оцениваются значением 0,638. Учитывая ошибки в оценке этого значения, для удобства можно принять градиент равным 2/3.
) показывает, что вполне допустимо рассматривать эти точки как лежащие на двух прямых линиях (рисунок Е.1). Расчеты, приведенные в Е.4, показывают, что градиенты этих линий одни и те же и оцениваются значением 0,638. Учитывая ошибки в оценке этого значения, для удобства можно принять градиент равным 2/3.
Одно и то же преобразование предназначено для повторяемости (сходимости) и воспроизводимости и выражено формулой
![]() . (3)
. (3)
Так как постоянным множителем можно пренебречь, то преобразование сводят к извлечению кубического корня из сообщенных результатов (бромных чисел). Выполнение этой процедуры дает преобразованные данные, приведенные в таблице Г.2, в которой результаты после извлечения кубического корня приведены с тремя значащими цифрами.
4.2 Выявление аномальных результатов
4.2.1 Сообщенные данные или, если принято решение о необходимости преобразования, преобразованные результаты изучают с целью выявления аномальных результатов. Они представляют собой значения, которые настолько отличаются от остальных, что единственное заключение, которое можно сделать, что они возникли вследствие ошибок в применении исследуемого метода или вследствие испытания по ошибке другой пробы. Можно использовать различные приемы, причем связанные с ними уровни значимости расходятся. Однако было найдено, что приемы, регламентированные в следующих разделах, являются подходящими для этого стандарта. Эти испытания основаны на предположении о нормальном распределении погрешностей [10].
4.2.2 Однородность данных, используемых для определения повторяемости (сходимости) метода
Первое испытание для выявления аномальных результатов касается обнаружения противоречивых данных в парах результатов, полученных при дублировании испытаний. Это испытание [3] включает расчет для всех комбинаций "лаборатория
проба". Далее для испытания отношения наибольшего из имеющегося набора
значений к сумме этих значений используют критерий Кохрена на 1%-ном уровне значимости (В.4). Если значение отношения превосходит критическое значение, приведенное в таблице Г.3 и соответствующее одной степени свободы (при этом
- число пар, которыми располагают при сравнении), тогда член пары, наиболее удаленный от среднего значения по пробе, должен быть отброшен. Процесс повторяют, уменьшая
на единицу, до тех пор, пока дальнейшее отбрасывание необходимо. В определенных случаях это испытание становится подобным "снежному кому" и приводит к неприемлемо большой доле аномальных результатов (более 10%). В этом случае следует отказаться от такого испытания по выявлению аномальных результатов, вернуть все или некоторые аномальные результаты для дальнейшей обработки и принять произвольное решение, основанное на ситуации.
Пример - В случае, относящемся к приведенному в таблице Г.2 примеру, абсолютные разности между преобразованными результатами повторных испытаний, т.е. парами чисел, рассчитанными с точностью до третьего десятичного знака, приведены в таблице 2.
Таблица 2
| Обозначение | Размах для пробы | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| А | 42 | 21 | 7 | 13 | 7 | 10 | 8 | 0 |
| В | 23 | 12 | 12 | 0 | 7 | 9 | 3 | 0 |
| С | 0 | 6 | 0 | 0 | 7 | 8 | 4 | 0 |
| D | 14 | 6 | 0 | 13 | 0 | 8 | 9 | 32 |
| Е | 65 | 4 | 0 | 0 | 14 | 5 | 7 | 28 |
| F | 23 | 20 | 34 | 29 | 20 | 30 | 43 | 0 |
| G | 62 | 4 | 78 | 0 | 0 | 16 | 18 | 56 |
| H | 44 | 20 | 29 | 44 | 0 | 27 | 4 | 32 |
| J | 0 | 59 | 0 | 40 | 0 | 30 | 26 | 0 |
Самый большой размах составляет 0,078 для лаборатории G на пробе 3. Сумма квадратов всех размахов составляет
0,042 + 0,021
+, ... , +0,026
+ 0
=0,0439.
В результате отношение, которое сравнивают с критическим значением в испытании по Кохрену, составляет
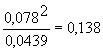 .
.
В примере используют 72 размаха, а в таблице Г.3 имеется критическое значение для 80 размахов, составляющее 0,1709. Следовательно, это отношение незначимо.
4.2.3 Однородность данных, используемых для определения воспроизводимости
4.2.3.1 Последующие испытания для выявления аномальных результатов относятся к установлению однородности данных, использованных при оценке воспроизводимости и предназначенных для обнаружения либо аномальной пары результатов от лаборатории на определенной пробе, либо аномальной серии результатов от какой-либо лаборатории на всех пробах. В обоих случаях подходящим оказывается испытание по Хокинсу [4].
Процедура включает образование среднего значения по каждой пробе или общего среднего по всем лабораториям по 4.5, образование отношения наибольшего абсолютного отклонения среднего значения пробы в лаборатории от среднего для пробы по всем лабораториям (или отклонение от среднего по всей таблице) к квадратному корню из соответствующих сумм квадратов по В.3.
4.2.3.2 Отношение, соответствующее наибольшему абсолютному отклонению, следует сравнивать с критическим значением на 1%-ном уровне значимости, приведенным в таблице Г.4. В этом случае представляет число ячеек-комбинаций "лаборатория
проба" для рассматриваемой пробы (или число средних по всем лабораториям), а
- число степеней свободы для суммы квадратов, которая является дополнением к квадрату, соответствующему рассматриваемой пробе. В испытании ячеек "лаборатория
проба"
относят к остальным пробам, однако в испытании средних значений по всем лабораториям
будет равно нулю.
4.2.3.3 Если значимый результат получают для отдельных проб, то соответствующие экстремальные значения следует отбросить, а процедуру испытания повторить. Если какие-либо экстремальные значения обнаружены среди итогов по лабораториям, то все результаты данной лаборатории следует отбросить.
Если доля брака при испытании высока (более 10%), то следует отказаться от такого испытания по выявлению аномальных результатов, вернуть все или некоторые аномальные результаты для дальнейшей обработки и принять произвольное решение, основанное на ситуации.
Пример - Применение испытания по Хокинсу к средним значениям по ячейкам для пробы.
Первый шаг состоит в том, чтобы рассчитать отклонения средних значений по ячейкам от соответствующих средних значений по пробам для всего массива данных.
Результаты, рассчитанные с точностью до третьего десятичного разряда, представлены в таблице 3.
Таблица 3
| Обозначение | Отклонение средних значений для пробы | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| А | 20 | 8 | 14 | 15 | 10 | 48 | 6 | 3 |
| В | 75 | 7 | 20 | 9 | 10 | 47 | 6 | 3 |
| С | 64 | 35 | 3 | 20 | 30 | 4 | 22 | 25 |
| D | 314 | 33 | 18 | 42 | 7 | 39 | 80 | 50 |
| Е | 32 | 32 | 30 | 9 | 7 | 18 | 18 | 39 |
| F | 75 | 97 | 31 | 20 | 30 | 8 | 74 | 53 |
| G | 10 | 34 | 32 | 20 | 20 | 61 | 9 | 62 |
| Н | 42 | 13 | 4 | 42 | 13 | 21 | 8 | 50 |
| J | 1 | 28 | 22 | 29 | 14 | 8 | 10 | 53 |
| Сумма квадратов | 117 | 15 | 4 | 6 | 3 | 11 | 13 | 17 |
В ходе расчета для каждой пробы вычисляют сумму квадратов отклонений. Эти результаты, также рассчитанные с точностью до единиц в третьем десятичном разряде, представлены в таблице 3.
В первую очередь испытывают ячейку с наибольшим экстремальным отклонением. Это отклонение получено лабораторией D на пробе 1.
Экспериментальное значение отношения в испытании по критерию Хокинса равно
![]() .
.
Критическое значение, соответствующее 9 ячейкам для пробы 1 и
=56 степеням свободы для других проб, получают путем интерполяции значений из таблицы Г.4, равным 0,3729. Экспериментальное значение больше критического, поэтому результаты испытаний, полученные в лаборатории D на пробе 1, отбрасывают.
Так как был отброшен аномальный результат, среднее значение, отклонения и сумму квадратов для пробы 1 пересчитывают, а процедуру выявления аномальных результатов повторяют.
Следующей испытываемой ячейкой является ячейка с результатом, полученным лабораторией F на пробе 2. Экспериментальное значение отношения в испытании по Хокинсу для этой ячейки составляет
![]() .
.
Критическое значение, соответствующее 9 ячейкам для пробы 1 и
=55 степеням свободы, соответствующим алгебраическому дополнению, получают путем интерполяции значений из таблицы Г.4 равным 0,3756. Так как экспериментальное значение меньше критического, то продолжать процедуру браковки не нужно.
4.3 Браковка полного набора данных по пробе
4.3.1 Межлабораторное среднеквадратическое отклонение и среднеквадратическое отклонение для повторных испытаний следует исследовать на предмет выявления "выпадающих" проб. Если исходные данные были подвергнуты преобразованию или какие-либо результаты были отброшены как аномальные, то следует вычислить новые значения среднеквадратических отклонений.
Если среднеквадратическое отклонение для какой-либо пробы оказывается исключительно большим, его следует исследовать с целью выявления необходимости браковки всех результатов испытаний этой пробы.
Для этого используют критерий Кохрена на 1%-ном уровне значимости, если среднеквадратические отклонения основаны на одинаковом числе степеней свободы. Испытание включает вычисление отношения наибольшей из соответствующих сумм квадратов (межлабораторных или для повторных испытаний в зависимости от ситуации) к их общей сумме по В.2. Если экспериментальное значение отношения превосходит критическое, приведенное в таблице Г.3 с в качестве числа проб и
в качестве степеней свободы для отдельного среднего квадратического отклонения, то все результаты для рассматриваемой пробы следует забраковать. В этом случае следует проверить, не обусловлено ли экстремальное среднеквадратическое отклонение применением неподходящего преобразования по 4.1 или необнаруженными аномальными результатами.
4.3.2 Не существует оптимального испытания для исследования однородности среднеквадратических отклонений, основанных на различных степенях свободы. Тем не менее распределение отношения максимальной дисперсии к дисперсии, средневзвешенной по всем остальным пробам, подчиняется F-распределению с и
степенями свободы (В.4). В этом случае
- степени свободы для дисперсии, о которой идет речь, а
- степени свободы взвешенной дисперсии для остальных проб. Если экспериментальное значение отношения больше критического, приведенного в таблицах Г.6.1-Г.6.5 и соответствующего уровню значимости 0,01/
, где
- число проб, то результаты для рассматриваемой пробы следует отвергнуть.
Пример - Среднеквадратические отклонения преобразованных результатов испытаний после отбраковки пары результатов, полученных в лаборатории D на пробе 1, приведены в таблице 4 в возрастающем порядке средних значений по пробам, скорректированных с точностью до трех значащих цифр после запятой. Соответствующие степени свободы приведены в скобках.
Таблица 4
| Наименование характеристики | Значение для пробы | |||||||
| 3 | 8 | 1 | 4 | 5 | 6 | 2 | 7 | |
| Среднее значение для пробы | 0,9100 | 1,066 | 1,240 | 1,538 | 2,217 | 3,639 | 4,028 | 4,851 |
| Межлабораторное среднеквадратическое отклонение | 0,0278 | 0,0473 | 0,0354 | 0,0297 | 0,0197 | 0,0378 | 0,0450 | 0,0416 |
| Среднеквадратическое отклонение для дублей | 0,0214 | 0,0182 | 0,0281 | 0,0164 | 0,0063 | 0,0132 | 0,0166 | 0,0130 |