ГОСТ Р 52736-2007
Группа Е09
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Короткие замыкания в электроустановках
МЕТОДЫ РАСЧЕТА ЭЛЕКТРОДИНАМИЧЕСКОГО
И ТЕРМИЧЕСКОГО ДЕЙСТВИЯ ТОКА КОРОТКОГО ЗАМЫКАНИЯ
Short-circuits in electrical installations.
Calculation methods of electrodynamics and thermal effects of short-circuit current
ОКС 29.020
Дата введения 2008-07-01
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. N 184-ФЗ "О техническом регулировании", а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 "Стандартизация в Российской Федерации. Основные положения"
Сведения о стандарте
1 РАЗРАБОТАН Филиалом ОАО "НТЦ электроэнергетики" - ВНИИЭ, Московским энергетическим институтом (Техническим университетом) (МЭИ (ТУ))
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 437 "Токи короткого замыкания"
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 12 июля 2007 г. N 174-ст
4 ВЗАМЕН ГОСТ Р 50254-92
Информация об изменениях к настоящему стандарту публикуется ежегодно в издаваемом информационном указателе "Национальные стандарты", а текст изменений и поправок - в ежемесячно издаваемых информационных указателях "Национальные стандарты". В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе "Национальные стандарты". Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
1 Область применения
1 Область применения
Настоящий стандарт распространяется на трехфазные электроустановки промышленной частоты и определяет методы расчета и проверки проводников и электрических аппаратов на электродинамическую и термическую стойкость при коротких замыканиях (КЗ).
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ГОСТ 687-78 Выключатели переменного тока на напряжение свыше 1000 В. Общие технические условия
ГОСТ 16442-80 Кабели силовые с пластмассовой изоляцией. Технические условия
ГОСТ 18410-73 Кабели силовые с пропитанной бумажной изоляцией. Технические условия
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю "Национальные стандарты", который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) документом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены следующие термины с соответствующими определениями:
3.1
| термическое действие тока короткого замыкания в электроустановке: Изменение температуры элементов электроустановки под действием тока короткого замыкания. |
3.2
| электродинамическое действие тока короткого замыкания в электроустановке: Механическое действие электродинамических сил, обусловленных током короткого замыкания, на элементы электроустановки. |
| 3.3 |
| интеграл Джоуля: Условная величина, характеризующая тепловое действие тока короткого замыкания на рассматриваемый элемент электроустановки, численно равная интегралу от квадрата тока короткого замыкания по времени, в пределах от начального момента короткого замыкания до момента его отключения. [ГОСТ 26522-85, статья 89] |
| 3.4 |
| ток термической стойкости электрического аппарата при коротком замыкании (ток термической стойкости): Нормированный ток, термическое действие которого электрический аппарат способен выдержать при коротком замыкании в течение нормированного времени термической стойкости. |
| 3.5 |
| ток электродинамической стойкости электрического аппарата при коротком замыкании (ток электродинамической стойкости): Нормированный ток, электродинамическое действие которого электрический аппарат способен выдержать при коротком замыкании без повреждений, препятствующих его дальнейшей работе. |
4 Общие положения
4.1 Исходные положения
4.1.1 При проверке проводников и электрических аппаратов электроустановок на электродинамическую и термическую стойкость при КЗ предварительно должны быть выбраны расчетные условия КЗ, т.е. расчетная схема электроустановки, расчетный вид КЗ в электроустановке, расчетная точка КЗ, а также расчетная продолжительность КЗ в электроустановке (последнюю используют при проверке на термическую стойкость проводников и электрических аппаратов, а также при проверке на невозгораемость кабелей).
4.1.2 Расчетная схема электроустановки должна быть выбрана на основе анализа возможных электрических схем этой электроустановки при продолжительных режимах ее работы. К последним следует относить также ремонтные и послеаварийные режимы работы.
4.1.3 В качестве расчетного вида КЗ следует принимать:
- при проверке электрических аппаратов и жестких проводников с относящимися к ним поддерживающими и опорными конструкциями на электродинамическую стойкость - трехфазное КЗ;
- при проверке электрических аппаратов и проводников на термическую стойкость - трех- или однофазное КЗ, а на генераторном напряжении электростанций - трех- или двухфазное КЗ, в зависимости от того, какое из них приводит к большему термическому воздействию;
- при проверке гибких проводников по условию их допустимого сближения во время КЗ - двухфазное КЗ.
4.1.4 В качестве расчетной точки КЗ следует принимать такую точку на расчетной схеме, при КЗ в которой проводник или электрический аппарат подвергается наибольшему электродинамическому или термическому воздействию.
Примечание - Исключения из этого требования допустимы лишь при учете вероятностных характеристик КЗ и должны быть обоснованы требованиями соответствующих ведомственных нормативных документов.
4.1.5 Расчетную продолжительность КЗ при проверке проводников и электрических аппаратов на термическую стойкость следует определять путем сложения времени действия основной релейной защиты, в зону которой входят проверяемые проводники и электрические аппараты, и полного времени отключения соответствующего выключателя, а при проверке кабелей на невозгораемость - путем сложения времени действия резервной релейной защиты и полного времени отключения ближайшего к месту КЗ выключателя.
При наличии устройств автоматического повторного включения (АПВ) цепи следует учитывать суммарное термическое действие тока КЗ.
4.1.6 При расчетной продолжительности КЗ до 1 с допустимо процесс нагрева проводников под действием тока КЗ считать адиабатическим, а при расчетной продолжительности КЗ более 1 с и при небыстродействующих АПВ следует учитывать теплоотдачу в окружающую среду.
5 Электродинамическое действие тока короткого замыкания
5.1 Расчет электродинамических сил взаимодействия проводников
5.1.1 Электродинамические силы взаимодействия 
, Н, двух параллельных проводников с токами следует определять по формуле
, (1)
где 
- постоянный параметр, Н/А
;
- мгновенные значения токов проводников, А;
- длина проводников, м;
- расстояние между осями проводников, м;
- коэффициент формы.
Для проводников прямоугольного сечения коэффициент формы следует определять по кривым, приведенным на рисунке 1.
Рисунок1 - Диаграмма для определения коэффициента формы проводников прямоугольного сечения
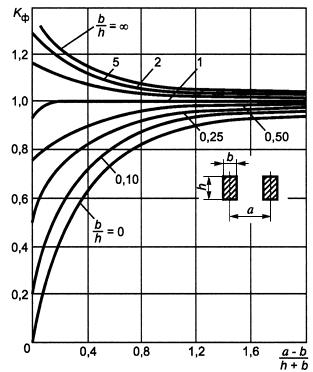
Рисунок 1 - Диаграмма для определения коэффициента формы проводников прямоугольного сечения
Для круглых проводников сплошного сечения, проводников кольцевого сечения, а также проводников (шин) корытообразного сечения с высотой профиля 0,1 м и более следует принимать =1,0.
5.1.2 Наибольшее значение электродинамической силы имеет место при ударном токе КЗ.
5.1.3 Максимальную силу 
, Н, (эквивалентную равномерно распределенной по длине пролета нагрузки), действующую в трехфазной системе проводников на расчетную фазу при трехфазном КЗ, следует определять по формуле
, (2)
где - длина пролета, м;
- ударный ток трехфазного КЗ, А;
- коэффициент, зависящий от взаимного расположения проводников.
Значения коэффициента 
для некоторых типов шинных конструкций (рисунок 2) указаны в таблице 1.
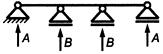
Рисунок 2 - Схемы взаимного расположения шинных конструкций
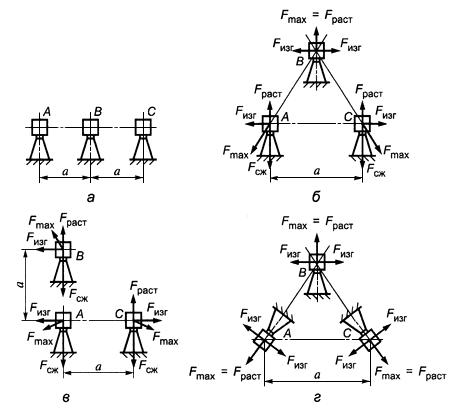
Рисунок 2 - Схемы взаимного расположения шинных конструкций
Таблица 1 - Значения коэффициента 
| Расположение шин | Расчетная фаза | Значение коэффициента | |||
| результирующей | изгибающей | растягивающей | сжимающей | ||
| В одной плоскости (рисунок 2 а) | В | 1,00 | 1,00 | 0 | 0 |
| По вершинам равностороннего треугольника (рисунок 2 б) | А | 1,00 | 0,94 | 0,25 | 0,75 |
| В | 1,00 | 0,50 | 1,00 | 0 | |
| | С | 1,00 | 0,94 | 0,25 | 0,75 |
| По вершинам прямоугольного равнобедренного треугольника (рисунок 2 в) | А | 0,87 | 0,87 | 0,29 | 0,87 |
| В | 0,95 | 0,43 | 0,83 | 0,07 | |
| | С | 0,95 | 0,93 | 0,14 | 0,43 |
| По вершинам равностороннего треугольника, но оси изоляторов расположены под углом 2 | А, В, С | 1,00 | 0,50 | 1,00 | 0 |
для нагрузок
/3 друг к другу (рисунок 2 г)
При двухфазном КЗ максимальную силу определяют по формуле
, (3)
где 
- ударный ток двухфазного КЗ, А.
5.2 Выбор расчетной механической схемы шинных конструкций и гибких проводников
5.2.1 Методику расчета электродинамической стойкости шинных конструкций и гибких проводников следует выбирать на основе расчетной механической схемы, учитывающей их особенности.
5.2.2 Следует различать:
- статические системы, обладающие высокой жесткостью, у которых шины и изоляторы при КЗ остаются неподвижными;
- динамические системы с жесткими опорами, у которых изоляторы при КЗ считаются неподвижными, а шины колеблются;
- динамические системы с упруго податливыми опорами, в которых при КЗ колеблются и шины, и опоры;
- динамические системы с гибкими проводниками.
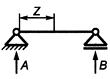
5.2.3 Расчетные механические схемы шинных конструкций различных типов, обладающих высокой жесткостью, представлены в таблице 2.
Таблица 2 - Расчетные схемы шинных конструкций
| Номер схемы | Расчетная схема | Тип балки и опоры | Коэффициент | ||
| | |
|
|
| |
| 1 |
| Однопролетная: | 8 | 1 | 3,14 |
| 2 |
| Однопролетная: | 8 | 1,25 | 3,93 |
| 3 |
| Однопролетная: | 12 | 1 | 4,73 |
| 4 |
| Двухпролетная: | 8 | 1,25 | 3,93 |
| 5 |
| Трех- и более пролетная: | 10* | 1,13 | |
| | А и В - простые опоры | 12** | 1 | 4,73 | |
| * Для крайних пролетов. | |||||
Расчетные схемы имеют вид равнопролетной балки, лежащей или закрепленной на жестких опорах и подвергающейся воздействию равномерно распределенной нагрузки.
Различают следующие типы шинных конструкций и соответствующих расчетных механических схем:
- шинная конструкция, длина которой равна длине одного пролета; для нее расчетной схемой является балка с шарнирным опиранием на обеих опорах пролета (таблица 2, схема N 1);
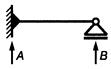
- шинная конструкция, длина которой равна длине одного пролета, с одной простой и одной неподвижной опорами; для нее расчетной схемой является балка с шарнирным опиранием на простой опоре и жестким опиранием (защемлением) на неподвижной опоре пролета (таблица 2, схема N 2);
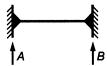
- шинная конструкция, длина которой равна длине одного пролета, с неподвижными опорами; для нее расчетной схемой является балка с жестким опиранием (защемлением) на обеих опорах пролета (таблица 2, схема N 3);
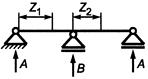
- шинные конструкции, длина которых равна длине двух, трех и более пролетов; для них расчетной схемой является балка с шарнирным опиранием на каждой из опор (таблица 2, схемы N 4 и 5).
5.2.4 Расчетной схемой шинной конструкции с упруго податливыми опорами следует считать схему, в которой масса шины распределена по длине пролета, а опоры представлены телами с эквивалентной массой 
и пружинами с жесткостью 
.
5.2.5 Для гибких проводников в качестве расчетной схемы применяют схему с жестким стержнем, ось которого очерчена по цепной линии. Гирлянды изоляторов вводят в механическую схему в виде жестких стержней, шарнирно соединенных с проводниками и опорами. Размеры стержней расчетной схемы определяют из статического расчета на действие сил тяжести.
5.3 Допустимые механические напряжения в материале проводников и механические нагрузки на опоры при коротком замыкании
5.3.1 Допустимое напряжение в материале жестких шин 
, Па, следует принимать равным 70% временного сопротивления разрыву материала шин 
. (4)
Допустимое напряжение в материале шин должно быть ниже предела текучести этого материала.
Временные сопротивления разрыву и допустимые напряжения в материалах шин приведены в таблице 3.
Таблица 3 - Основные характеристики материалов шин
| Материал шины | Марка | Временное сопротивление разрыву, МПа | Допустимое напряжение, МПа | Модуль упругости, 10 | ||
| материала | в области сварного соединения | материала | в области сварного соединения | |||
| Алюминий | АО, А | 118 | 118 | 82 | 82 | 7 |
| АДО | 59-69 | 59-69 | 41-48 | 41-48 | 7 | |
| Алюминиевый сплав | АД31Т | 127 | 120 | 89 | 84 | 7 |
| АД31Т1 | 196 | 120 | 137 | 84 | 7 | |
| АВТ1 | 304 | 152 | 213 | 106 | 7 | |
| 1915Т | 353 | 318 | 247 | 223 | 7 | |
| Медь | МГМ | 245-255 | - | 171,5-178 | - | 10 |
| МГТ | 245-294 | - | 171,5-206 | - | 10 | |
Па
В зоне сварных соединений шин их временное сопротивление разрыву снижается. Его значение обычно определяют экспериментально; при отсутствии экспериментальных данных значения временного сопротивления разрыву, а также допустимого напряжения следует принимать, используя данные таблицы 3.
5.3.2 В зависимости от взаимного расположения шин и изоляторов последние при воздействии на них электродинамических сил работают на изгиб или растяжение (сжатие) или одновременно на изгиб и растяжение (сжатие). В общем случае допустимую нагрузку на изолятор (изоляционную опору) 
следует принимать равной 60% минимальной разрушающей нагрузки 
, приложенной к вершине изолятора (опоры) при изгибе или разрыве
. (5)
5.3.3 В случае работы изолятора на изгиб или растяжение (сжатие) значения допустимых нагрузок на изолятор (опору) 
и 
, Н, следует принимать соответственно равными:
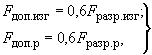(6)
где 
и 
- задаваемые предприятием-изготовителем минимальные разрушающие нагрузки соответственно при изгибе и растяжении (сжатии) изолятора, Н.
5.3.4 Допустимую нагрузку на спаренные изоляторы (опоры) следует принимать равной 50% суммарного разрушающего усилия изоляторов (опор)
, (7)
где 
- суммарное разрушающее усилие спаренных изоляторов (опор), Н.
5.3.5 При удалении центра масс шины от вершины опорного изолятора, например, когда плоская шина поставлена на ребро (рисунок 3а, б), значение допустимой нагрузки на опорный изолятор при изгибе следует пересчитать в соответствии с формулой
, (8)
где 
- коэффициент допустимой нагрузки, равный 0,6 или 0,5 (5.3.2-5.3.4);
и 
- расстояния от опасного сечения изолятора соответственно до его вершины и центра масс поперечного сечения шины, м.
Опасное сечение опорно-стержневых изоляторов с внутренним креплением арматуры (рисунок 3а) следует принимать у опорного фланца, опорно-стержневых изоляторов с внешним креплением арматуры (рисунок 3б, в) - у кромки нижнего фланца, а опорно-штыревых изоляторов (рисунок 3г) - на границе контакта штыря с фарфоровым телом изолятора.
Допустимую изгибающую нагрузку многоярусных изоляционных опор (колонок изоляторов) (рисунок 3г, д) следует принимать равной допустимой нагрузке наименее прочного яруса, определяемой по формуле (8).
Рисунок 3 - Определение допустимых нагрузок на изоляторы и изоляционные опоры
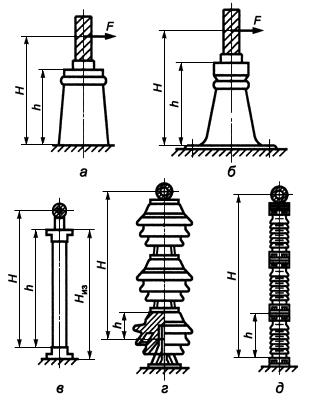
Рисунок 3 - Определение допустимых нагрузок на изоляторы и изоляционные опоры
5.3.6 При расположении фаз по вершинам треугольника (рисунок 2б, в, г) изоляторы одновременно испытывают как растягивающие (сжимающие), так и изгибающие усилия. Допустимые изгибающую 
и растягивающую 
нагрузки в ньютонах следует определять по формулам (6).
5.3.7 Допустимое напряжение в материале гибких проводников , МПа, следует принимать равным
, (9)
где - коэффициент допустимой нагрузки, равный 0,35-0,50;
- предел прочности при растяжении, Н.
5.3.8 Допустимую нагрузку на подвесные изоляторы следует принимать равной 30% разрушающей нагрузки, т.е.
. (10)
5.3.9 Расстояния между проводниками фаз 
, а также между проводниками и заземленными частями 
шинных конструкций напряжением 35 кВ и выше и проводников ошиновки распределительных устройств и воздушных линий, а также токопроводов к моменту отключения КЗ должны оставаться больше допустимых изоляционных расстояний, определяемых при рабочих напряжениях, т.е.
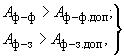(11)
где 
и 
- минимально допустимые расстояния по условиям пробоя соответственно между проводниками фаз и проводниками и заземленными частями при рабочем напряжении.
5.4 Определение механических напряжений в материале проводников и механических нагрузок на опоры при коротком замыкании
5.4.1 Расчет шинных конструкций, обладающих высокой жесткостью
5.4.1.1 При расчете шинной конструкции, обладающей высокой жесткостью, шину в любом пролете между изоляторами, кроме крайних, следует рассматривать как стержень (балку). Наличие ответвлений допускается не учитывать.
5.4.1.2 Максимальное напряжение в материале шины 
, Па, и нагрузку на изолятор шинной конструкции высокой жесткости 
, Н, при трехфазном КЗ следует определять по формулам:
; (12)
, (13)
где - максимальная сила, возникающая в многопролетной балке при трехфазном КЗ, Н, определяемая по формуле (2);
- длина пролета, м;
и 
- коэффициенты, зависящие от условия опирания (закрепления) шин, а также числа пролетов конструкции с неразрезными шинами (таблица 2);
- момент сопротивления поперечного сечения шины, м
; формулы для его расчета приведены в таблице 4.
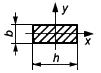
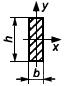
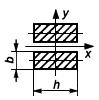
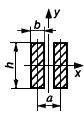
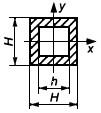
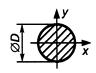
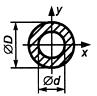
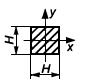
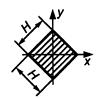
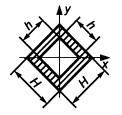
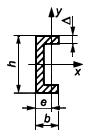
Таблица 4 - Формулы для определения момента инерции 
и момента сопротивления поперечных сечений шин
| Форма поперечного сечения и расположение шин | Расчетные формулы | |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Примечание - Когда прокладки приварены к обеим полосам пакета, то вместо формул, отмеченных * и **, следует применять формулы: | ||
,
; 
;
; 
.
При двухфазном КЗ
; (14)
, (15)
где 
- максимальная сила, возникающая в многопролетной балке при двухфазном КЗ, Н, и определяемая по формуле (3).
При расчете напряжений в области сварных соединений, находящихся на расстоянии 
от опорного сечения, в формулы (12) и (14) следует подставлять значения 
, вычисленные в соответствии с таблицей А.1 (приложение А).
5.4.1.3 Электродинамические нагрузки на отдельные проводники составных шин (рисунок 4) обусловлены взаимодействием их токов с токами проводников других фаз и с токами других элементов проводника одной и той же фазы. Максимальное напряжение в материале составных шин при КЗ допускается определять по формуле
, (16)
где 
- максимальное напряжение в материале шины, обусловленное взаимодействием тока данного проводника с токами проводников других фаз, Па, которое в зависимости от вида КЗ следует определять по формулам (12) или (14);
- максимальное напряжение в материале шины, обусловленное взаимодействием токов отдельных элементов проводника одной фазы, Па, которое следует определять по формуле
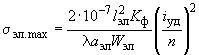, (17)
где 
- расстояние между осями прокладок, м;
- расстояние между осями поперечных сечений элементов составных шин, м (рисунок 4);
- момент сопротивления поперечного сечения элемента составной шины, м;
- ударный ток трехфазного или двухфазного КЗ, А;
- число проводников в одной фазе.
Рисунок 4 - Двухполосная шина
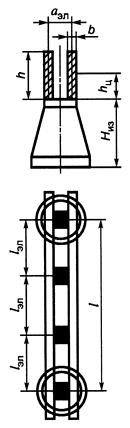
Рисунок 4 - Двухполосная шина
5.4.2 Расчет шинных конструкций с жесткими опорами
5.4.2.1 Шинную конструкцию, изоляторы которой обладают высокой жесткостью, в расчетах на динамическую стойкость при КЗ следует представлять как стержень с защемленными концами, имеющий лишь основную частоту собственных колебаний.
5.4.2.2 Максимальное напряжение в материале шин , Па, и нагрузку на изоляторы 
, H, при расположении шин в одной плоскости и высокой жесткости изоляторов шинной конструкции следует определять по формулам:
при трехфазном КЗ
; (18)
; (19)
при двухфазном КЗ
; (20)
, (21)
где 
- коэффициент динамической нагрузки, зависящий от основной частоты собственных колебаний шины 
(5.4.2.3) и от ударного коэффициента тока 
. Значения коэффициента для двухфазного и трехфазного КЗ в зависимости от отношения 
(
=50 Гц) при разных коэффициентах следует определять по графикам, приведенным на рисунке 5.
Рисунок 5 - Зависимость коэффициента динамической нагрузки для изоляторов и шин от частоты собственных колебаний шины при различных ударных коэффициентах
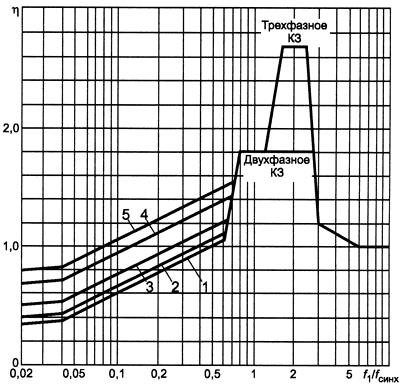
Рисунок 5 - Зависимость коэффициента динамической нагрузки для изоляторов и шин от частоты собственных колебаний шины при различных ударных коэффициентах : 1- 
1,6; 2-=1,4; 3-=1,25; 4-=1,1; 5-=1,0
5.4.2.3 Расчетную частоту собственных колебаний шины , Гц, следует определять по формуле
, (22)
где 
- параметр основной частоты собственных колебаний шины. Значения этого параметра зависят от типа шинной конструкции и указаны в таблице 2;
- модуль упругости материала шины, Па;
- момент инерции поперечного сечения шины, м
;
- масса шины на единицу длины, кг/м.
5.4.2.4 Максимальную нагрузку на проходные изоляторы , Н, следует определять по формуле
, (23)
где 
- расстояние от торца проходного изолятора до ближайшего опорного изолятора фазы, м.
5.4.2.5 Максимальное напряжение (Па) в материале составных шин шинной конструкции с жесткими опорами допустимо определять по формуле (16). При этом максимальное напряжение в материале шин, обусловленное взаимодействием проводников других фаз, 
, следует определять в зависимости от вида КЗ по формуле (18) или (20), а максимальное напряжение в материале шин, обусловленное взаимодействием отдельных элементов проводника одной фазы, 
, - по формуле
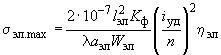, (24)
где 
- коэффициент динамической нагрузки, зависящий от расчетной основной частоты собственных колебаний элементов составной шины 
, который следует определять по расчетным графикам, приведенным на рисунке 5.
Расчетную основную частоту собственных колебаний элементов составной шины фазы , Гц, определяют по формуле
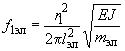, (25)
где 
- расстояние между осями прокладок, м;
- момент инерции поперечного сечения элемента шины, м;
- масса элемента шины на единицу длины, кг/м.
5.4.2.6 Максимальное напряжение в материале шин , Па, и максимальную нагрузку на опорные и проходные изоляторы , H, при расположении шин по вершинам треугольника (рисунок 2б, в, г) следует определять с учетом их пространственных колебаний, используя формулы:
; (26)
; (27)
, (28)
где - меньший из двух моментов сопротивления поперечного сечения шины, м, т.е. момента сопротивления при изгибе в плоскости, проходящей через ось изоляторов, и момента сопротивления при изгибе шины в плоскости, проходящей через другую ось шины;
и - электродинамические силы, определяемые соответственно по формулам (2) и (3);
и 
- коэффициенты, значения которых для наиболее распространенных типов шинных конструкций (рисунок 2, б, в, г) приведены в таблице 5.
Таблица 5 - Значения коэффициентов и шинных конструкций
| Расположение шин | Схема конструкции на рисунке 2 | Значение коэффициента | Значение коэффициента | |
| для шин круглого и кольцевого сечений | для шин квадратного сечения | |||
| По вершинам прямоугольного равнобедренного треугольника | в | 0,95 | 0,95 | 1,16 |
| По вершинам равностороннего треугольника | б | 1,0 | 1,0 | 1,39 |
| г | 1,0 | 1,0 | 1,21 | |