ГОСТ Р 50779.21-2004
Группа Т59
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ПРАВИЛА ОПРЕДЕЛЕНИЯ И МЕТОДЫ РАСЧЕТА
СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ПО ВЫБОРОЧНЫМ ДАННЫМ
Часть 1
Нормальное распределение
Statistical methods. Determination rules and methods
for calculation of statistical characteristics based on sample data.
Part 1. Normal distribution
ОКС 03.120.30
Дата введения 2004-06-01
Предисловие
1 РАЗРАБОТАН Техническим комитетом по стандартизации ТК 125 "Статистические методы в управлении качеством продукции"
2 ВНЕСЕН Научно-техническим управлением Госстандарта России
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 12 января 2004 г. N 3-ст
4 Настоящий стандарт разработан с учетом основных нормативных положений международного стандарта ИСО 2854:1976 "Статистическое представление данных. Методы оценки и проверки гипотез о средних значениях и дисперсиях" (ISO 2854:76 "Statistical interpretation of data - Techniques of estimation and tests relating to means and variance", NEQ)
5 ВЗАМЕН ГОСТ Р 50779.21-96
Информация об изменениях к настоящему стандарту публикуется в указателе "Национальные стандарты", а текст этих изменений - в информационных указателях "Национальные стандарты". В случае пересмотра или отмены настоящего стандарта соответствующая информация будет опубликована в информационном указателе "Национальные стандарты"
Введение
Введение
Стандарт устанавливает процедуры и методы решения ряда практических задач статистики в случае, когда наблюдаемые величины являются случайными и распределены по нормальному закону.
В стандарте изложены методы решения следующих задач:
а) точечного оценивания параметров нормального распределения случайной величины;
б) точечного оценивания вероятности попадания (доли распределения) случайной величины в заданный интервал и вне его;
в) интервального (доверительного) оценивания параметров нормального распределения и доли распределения;
г) проверки гипотез об этих же величинах.
Все процедуры, приведенные в стандарте, используют ограниченный ряд статистически независимых наблюдений, полученных в производстве, в лабораторных условиях, при контроле, измерении, оценке и т.п.
1 Область применения
Настоящий стандарт устанавливает методы, применяемые для:
- оценки математического ожидания и дисперсии генеральной совокупности;
- проверки гипотез относительно значений этих параметров;
- оценки вероятности попадания (доли распределения) случайной величины в заданный интервал.
Примечание - Вероятность попадания случайной величины в интервал равна доле распределения случайной величины в этом интервале. В большинстве практических задач физический смысл имеет понятие "доля распределения случайной величины в интервале", которое далее применено в настоящем стандарте.
Методы, изложенные в настоящем стандарте, применимы в том случае, если выполнены следующие условия:
- элементы выборки получены путем независимых повторений эксперимента. В случае конечной генеральной совокупности объем выборки должен составлять не более 10% объема генеральной совокупности;
- наблюдаемые переменные распределены по нормальному закону. Однако если распределение вероятностей несильно отличается от нормального, то описанные в стандарте методы остаются применимыми для большинства практических приложений. В этом случае объем выборки должен быть не менее 10 единиц, причем достоверность получаемых статистических выводов возрастает при увеличении объемов выборок.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения
ГОСТ Р 50779.11-2000 (ИСО 3534-2-93) Статистические методы. Статистическое управление качеством. Термины и определения
Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов по указателю "Национальные стандарты", составленному по состоянию на 1 января текущего года, и по соответствующим информационным указателям, опубликованным в текущем году. Если ссылочный документ заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться замененным (измененным) стандартом. Если ссылочный документ отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.
3 Термины и определения
В настоящем стандарте применены термины по ГОСТ Р 50779.10 и ГОСТ Р 50779.11, а также следующие термины с соответствующими определениями:
3.1 точечное оценивание параметра: Получение оценки параметра в виде одного численного значения;
3.2 интервальное (доверительное) оценивание параметра: Получение оценки параметра в виде доверительного интервала;
3.3 доверительный интервал: Интервал, границы которого являются функциями от выборочных данных и который накрывает истинное значение оцениваемого параметра с вероятностью не менее 1- (где 1-
- доверительная вероятность).
Примечание - Доверительный интервал может быть двусторонним или односторонним;
3.4 нулевая гипотеза: Предположение о распределении генеральной совокупности, которое проверяют по статистическим данным.
Примечание - В частности, в настоящем стандарте рассмотрены предположения о значениях параметров распределения.
4 Обозначения
| В настоящем стандарте применены следующие обозначения: | |
|
| математическое ожидание нормального закона распределения (среднее значение генеральной совокупности, далее - среднее значение); |
|
| известное значение параметра |
|
| математические ожидания для двух различных генеральных совокупностей; |
|
| точечная оценка параметра |
|
| верхняя и нижняя доверительные границы параметра |
|
| точечная оценка разности значений параметров |
|
| стандартное (среднеквадратичное) отклонение нормально распределенной случайной величины; |
|
| дисперсия генеральной совокупности; |
|
| известное значение дисперсии генеральной совокупности, |
|
| известное численное значение параметра |
|
| известные значения параметров |
|
| точечная оценка параметра |
|
| верхняя и нижняя доверительные границы параметра |
|
| точечная оценка дисперсии; |
|
| выборочное значение наблюдаемой случайной величины; |
|
| выборочное значение случайной величины из первой генеральной совокупности; |
|
| то же, из второй генеральной совокупности; |
|
| объемы выборок; |
|
| среднеарифметические значения (выборочные средние); |
|
|
|
|
| то же для двух выборок соответственно; |
|
| риск первого рода (вероятность отвергнуть гипотезу, когда она верна); |
|
| уровень значимости при проверке гипотез, а также доверительная вероятность |
|
| число степеней свободы; |
|
| квантили стандартного нормального закона распределения уровней |
|
| квантили распределения Стьюдента с |
|
| квантиль распределения Фишера с |
|
| квантили |
|
| нижняя и верхняя границы интервала соответственно; |
|
| доля распределения (вероятность попадания) случайной величины в заданный интервал |
|
| доля распределения (вероятность попадания) случайной величины вне интервала |
|
| точечные оценки |
|
| нижние односторонние доверительные границы для |
|
| верхние односторонние доверительные границы для |
|
| случайное событие: например, попадание случайной величины в заданный интервал; |
|
| вероятность случайного события |
|
| сумма выборочных значений. |
5 Общие требования
5.1 Настоящий стандарт содержит описание типовых статистических задач, а также процедур, при помощи которых они решаются. Представленные задачи могут быть разбиты на три класса:
- точечное и интервальное оценивание среднего значения генеральной совокупности;
- точечное и интервальное оценивание дисперсии генеральной совокупности;
- точечное и интервальное оценивание доли распределения (вероятность попадания) случайной величины в заданном интервале и вне его.
5.2 Для решения каждой из перечисленных задач по 5.1 приведены процедуры их решения (разделы 6, 7, 8), включающие в себя:
1) статистические и исходные данные;
2) определение стандартных табличных данных, которые необходимы для проведения вычислений (приложения А, Б, В, Г), а также проведение вычислений параметров коэффициентов по приведенным формулам;
3) результаты, полученные в итоге проведенных вычислений.
5.3 Для задач каждого класса приведены примеры их применения на практике (в производстве, медицине, химии). Спектр возможных применений этих задач не ограничивается приведенными в разделах 6, 7, 8 примерами.
5.4 Во всех приведенных задачах предполагается, что статистические и исходные данные подчиняются нормальному закону распределения. В тех случаях, когда изначально в этом нет достаточной уверенности, должны быть проведены предварительные исследования соответствия исходных данных нормальному закону.
5.5 Процедуры решения перечисленных в 5.1 задач представлены в таблицах, соответствующих этим задачам (разделы 6, 7, 8).
Номера таблиц разделов 6, 7, 8 для решения соответствующих задач перечислены в обобщенных таблицах 5.1, 5.2, 5.3, 5.4.
Таблица 5.1 - Номера таблиц для решения задач по оценке среднего значения (раздел 6)
| Задача оценки среднего значения | Номер таблицы | |
| |
|
|
| Оценка среднего | 6.1 | 6.2 |
| Сравнение среднего значения с заданным значением | 6.3 | 6.4 |
| Сравнение двух средних | 6.5 | 6.6 |
| Оценка разности двух средних | 6.7 | 6.8 |
Таблица 5.2 - Номера таблиц для решения задач по оценке дисперсии (раздел 7)
| Задача оценки дисперсии | Номер таблицы |
| Оценка дисперсии | 7.1 |
| Сравнение дисперсии или стандартного отклонения с заданным значением | 7.2 |
| Сравнение двух дисперсий или двух стандартных отклонений | 7.3 |
Таблица 5.3 - Номера таблиц для решения задач по точечной оценке доли распределения случайной величины в заданном интервале (раздел 8)
| Номер таблицы | |
|
|
|
| 8.2 | 8.3 |
Таблица 5.4 - Номера таблиц для решения задач по интервальной оценке доли распределения случайной величины при неизвестной дисперсии в заданном интервале (раздел 8)
| Заданные границы интервала | Искомая величина | Номер таблицы |
| |
| 8.4 |
| |
| 8.5 |
|
|
| 8.6 |
| |
| 8.7 |
| |
| 8.8 |
|
|
| 8.9 |
5.6 Процедуры интервального оценивания доли распределения случайной величины в заданном интервале, изложенные в разделе 8 настоящего стандарта, являются простыми для применения, но не самыми эффективными. Более эффективными являются процедуры с использованием таблиц нецентрального распределения Стьюдента или таблиц толерантных множителей, которые в настоящем стандарте не приведены.
6 Точечное и интервальное оценивание математического ожидания генеральной совокупности
6.1 Алгоритм точечного и интервального оценивания среднего значения при известной дисперсии приведен в таблице 6.1.
Таблица 6.1 - Оценка среднего значения при известной дисперсии
| Статистические и исходные данные | Табличные данные и вычисления |
| 1 Объем выборки: | 1 Квантиль стандартного нормального закона распределения уровня |
| |
|
| 2 Сумма значений наблюдаемых величин: | 2 Квантиль стандартного нормального закона распределения уровня |
|
|
|
| 3 Известное значение дисперсии: | 3 Вычисляем: |
| |
|
| 4 Выбранная доверительная вероятность: | 4 Вычисляем: |
|
|
|
| 5 Вычисляем: | |
| |
|
| Результаты | |
| 1 Точечная оценка параметра | |
|
| |
| 2 Двусторонний симметричный доверительный интервал для | |
|
| |
| 3 Односторонние доверительные интервалы для | |
|
| |
|
| |
|
| |
Примеры
1 Определение настроенности станка-автомата при механической обработке (например, токарного, шлифовального). Точность станка, определяемая разбросом получаемых размеров деталей без изменения настройки, считается известной, а центр настройки требуется определить. Возможны оценки в виде точечного значения
или в виде интервала, который с известной степенью доверия (доверительной вероятностью) включает неизвестное значение
. Интервал может быть:
- двусторонним, если необходима уверенность с заданной доверительной вероятностью, в каких пределах может лежать ;
- односторонним с верхней границей, если необходима уверенность, что не выше какого-то значения;
- односторонним с нижней границей, если необходима уверенность, что не ниже какого-то значения.
2 Оценка настройки автоматического оборудования для розлива жидкости в тару. Условие и возможные типы оценок - как в примере 1.
3 Многие другие технологические процессы с известной или оцененной заранее точностью (т.е. известным параметром ), в которых выходной контролируемый параметр имеет равновозможные отклонения в большую или меньшую стороны от центра настройки
. Условие и возможные типы оценок - как в примере
6.2 Алгоритм точечного и интервального оценивания среднего значения при неизвестной дисперсии приведен в таблице 6.2.
Таблица 6.2 - Оценка среднего значения при неизвестной дисперсии
| Статистические и исходные данные | Табличные данные и вычисления |
| 1 Объем выборки: | 1 Квантиль распределения Стьюдента уровня |
| |
|
| 2 Сумма значений наблюдаемых величин: | 2 Квантиль распределения Стьюдента уровня |
|
|
|
| 3 Сумма квадратов значений наблюдаемых величин: | 3 Вычисляем: |
|
|
|
| 4 Степени свободы: | 4 Вычисляем: |
|
|
|
| 5 Выбранная доверительная вероятность: | 5 Вычисляем: |
|
|
|
| | 6 Вычисляем: |
| |
|
| | 7 Вычисляем: |
| |
|
| Результаты | |
| 1 Точечная оценка параметра | |
|
| |
| 2 Точечная оценка параметра | |
|
| |
| 3 Двусторонний симметричный доверительный интервал для параметра | |
|
| |
| 4 Односторонние доверительные интервалы для параметра | |
|
| |
| или | |
|
| |
| Примечание - Квантили распределения Стьюдента определяют по таблице Б.1 приложения Б. | |
Примеры - Примеры те же, что в 6.1, но точность, определяемая разбросом контролируемых значений, заранее неизвестна.
6.3 Алгоритм решения задачи сравнения неизвестного среднего значения с заданным значением при известной дисперсии приведен в таблице 6.3.
Таблица 6.3 - Сравнение неизвестного среднего значения с заданным значением при известной дисперсии
| Статистические и исходные данные | Табличные данные и вычисления |
| 1 Объем выборки: | 1 Квантиль стандартного нормального закона распределения уровня |
| |
|
| 2 Сумма значений наблюдаемых величин: | 2 Квантиль стандартного нормального закона распределения уровня |
|
|
|
| 3 Заданное значение: | 3 Вычисляем: |
| |
|
| 4 Известное значение дисперсии генеральной совокупности: | |
| | |
| или стандартного отклонения: | |
| | |
| 5 Выбранный уровень значимости: | |
| | |
| Результаты | |
| Сравнение выборочного среднего значения | |
| 1 В двустороннем случае: | |
| Предположение равенства выборочного среднего и заданного значений (нулевая гипотеза) отклоняется, если: | |
|
| |
| 2 В одностороннем случае: | |
| а) предположение о том, что выборочное среднее не менее чем | |
|
| |
| б) предположение о том, что выборочное среднее не более чем | |
|
| |
| Примечание - Квантили стандартного нормального закона распределения определяют по таблице А.1 приложения А. | |
Пример - Проверка правильности настройки технологического процесса на середину поля допуска или на заданное оптимальное значение. Точность технологического процесса предполагается известной или заранее оцененной, т.е. значение известно.
Возможные технологические процессы: механическая обработка, расфасовка и другие, где равновозможны отклонения контролируемого параметра в большую и меньшую сторону от центра настройки.
6.4 Алгоритм решения задачи сравнения неизвестного среднего значения с заданным значением при неизвестной дисперсии приведен в таблице 6.4.
Таблица 6.4 - Сравнение неизвестного среднего значения с заданным значением при неизвестной дисперсии
| Статистические и исходные данные | Табличные данные и вычисления |
| 1 Объем выборки: | 1 Квантиль распределения Стьюдента уровня |
| |
|
| 2 Сумма значений наблюдаемых величин: | 2 Квантиль распределения Стьюдента уровня |
|
|
|
| 3 Сумма квадратов значений наблюдаемых величин: | 3 Вычисляем: |
|
|
|
| 4 Заданное значение: | 4 Вычисляем: |
| |
|
| 5 Степени свободы: | 5 Вычисляем: |
|
|
|
| 6 Выбранный уровень значимости: | |
| | |
| Результаты | |
| Сравнение выборочного среднего значения | |
| 1 В двустороннем случае: | |
| Предположение равенства выборочного среднего и заданного значений (нулевая гипотеза) отклоняется, если: | |
|
| |
| 2 В одностороннем случае: | |
| а) предположение о том, что выборочное среднее не менее чем | |
|
| |
| б) предположение о том, что выборочное среднее не более чем | |
|
| |
| Примечание - Квантили распределения Стьюдента определяют по таблице Б.1 приложения Б. | |
Примеры
1 То же, что в примере 6.3, но точность технологического процесса заранее неизвестна.
2 Контрольные проверки в розничной торговле и сфере обслуживания.
Например, у пяти человек, купивших по 1 кг сливочного масла, проводят повторное взвешивание товара на контрольных, более точных весах. При этом должен быть получен ответ на вопрос: являются ли отклонения от точного веса случайными или имеется систематическое обвешивание покупателей.
То же - при отпуске бензина и масел на автозаправочных станциях, то же - при продаже тканей в магазинах и т.п.
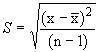 -
-