ГОСТ 8.207-76
Государственная система обеспечения единства измерений. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения

ГОСТ 8.207-76
Группа Т80

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР


Государственная система обеспечения единства измерений

ПРЯМЫЕ ИЗМЕРЕНИЯ С МНОГОКРАТНЫМИ НАБЛЮДЕНИЯМИ.
МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ

Основные положения

State system for ensuring the uniformity of measurements.
Direct measurements with multiple observations.
Methods of processing the results of observations.
Basic principles

Дата введения 1977-01-01

УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ постановлением Государственного комитета стандартов Совета Министров СССР от 15 марта 1976 г. N 619

ПЕРЕИЗДАНИЕ. Август 1985 г.


Настоящий стандарт распространяется на нормативно-техническую документацию, предусмотренную ГОСТ 8.010-72 и регламентирующую методику выполнения прямых измерений с многократными независимыми наблюдениями, и устанавливает основные положения методов обработки результатов наблюдений и оценивания погрешностей результатов измерений.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. При статистической обработке группы результатов наблюдений следует выполнить следующие операции:

исключить известные систематические погрешности из результатов наблюдений;

вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;

вычислить оценку среднего квадратического отклонения результата наблюдения;

вычислить оценку среднего квадратического отклонения результата измерения;

проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению;

вычислить доверительные границы случайной погрешности (случайной составляющей погрешности) результата измерения;

вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения;

вычислить доверительные границы погрешности результата измерения.

1.2. Проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, следует проводить с уровнем значимости от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений.

1.3. Для определения доверительных границ погрешности результата измерения доверительную вероятность принимают равной 0,95.

В тех случаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности =0,95, допускается указывать границы для доверительной вероятности =0,99.

В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо =0,99 принимать более высокую доверительную вероятность.

2. РЕЗУЛЬТАТ ИЗМЕРЕНИЯ И ОЦЕНКА ЕГО СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ

2.1. Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений.

Если результаты наблюдений можно считать принадлежащими к нормальному распределению, грубые погрешности исключают в соответствии с указаниями, приведенными в ГОСТ 11.002-73.

2.2. За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения систематических погрешностей.

Примечание. Если во всех результатах наблюдений содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.

2.3. Среднее квадратическое отклонение результата наблюдения оценивают согласно разд. 1 ГОСТ 11.004-74.

2.4. Среднее квадратическое отклонение () результата измерения оценивают по формуле

,

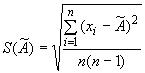где - -й результат наблюдения;

- результат измерения (среднее арифметическое исправленных результатов наблюдений);

- число результатов наблюдений;

- оценка среднего квадратического отклонения результата измерения.

3. ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ СЛУЧАЙНОЙ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

3.1. Доверительные границы случайной погрешности результата измерения в соответствии с настоящим стандартом устанавливают для результатов наблюдений, принадлежащих нормальному распределению.

Если это условие не выполняется, методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

3.1.1. При числе результатов наблюдений > 50 для проверки принадлежности их к нормальному распределению по ГОСТ 11.006-74 предпочтительным является один из критериев: Пирсона или Мизеса-Смирнова.

3.1.2. При числе результатов наблюдений 50>>15 для проверки принадлежности их к нормальному распределению предпочтительным является составной критерий, приведенный в справочном приложении 1.

При числе результатов наблюдений 15 принадлежность их к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности результата измерения по методике, предусмотренной настоящим стандартом, возможно в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

3.2. Доверительные границы (без учета знака) случайной погрешности результата измерения находят по формуле

,

где - коэффициент Стьюдента, который в зависимости от доверительной вероятности и числа результатов наблюдений находят по таблице справочного приложения 2.

4. ДОВЕРИТЕЛЬНЫЕ ГРАНИЦЫ НЕИСКЛЮЧЕННОЙ СИСТЕМАТИЧЕСКОЙ ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

4.1. Неисключенная систематическая погрешность результата образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности:

метода;

средств измерений;

вызванные другими источниками.

В качестве границ составляющих неисключенной систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

4.2. При суммировании составляющих неисключенной систематической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величины. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.

4.3. Границы неисключенной систематической погрешности результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измерений, метода и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле

,

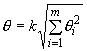где - граница -й неисключенной систематической погрешности;

- коэффициент, определяемый принятой доверительной вероятностью. Коэффициент принимают равным 1,1 при доверительной вероятности =0,95.

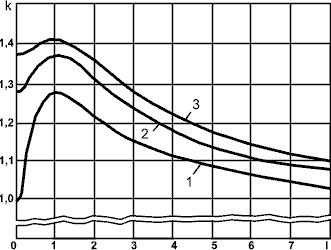
При доверительной вероятности =0,99 коэффициент принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (>4). Если же число суммируемых погрешностей равно четырем или менее четырех (4), то коэффициент определяют по графику зависимости (см. чертеж).

,

где - число суммируемых погрешностей;

; кривая 1-m = 2; кривая 2-m = 3; кривая 3-m = 4.

График зависимости k=f(m,l)

График зависимости

При трех или четырех слагаемых в качестве принимают составляющую, по числовому значению наиболее отличающуюся от других, в качестве следует принять ближайшую к составляющую.

Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что при вычислении доверительных границ случайной погрешности результата измерения.

5. ГРАНИЦА ПОГРЕШНОСТИ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ

5.1. В случае, если <0,8, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата . Если >8, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что граница погрешности результата .

Примечание. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15%.

5.2. В случае, если неравенства п. 5.1 не выполняются, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисключенных систематических погрешностей, рассматриваемых как случайные величины в соответствии с п. 4.3. Если доверительные границы случайных погрешностей найдены в соответствии с разд. 3 настоящего стандарта, допускается границы погрешности результата измерения (без учета знака) вычислить по формуле

,

где - коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;

- оценка суммарного среднего квадратического отклонения результата измерения.

Оценку суммарного среднего квадратического отклонения результата измерения вычисляют по формуле

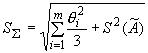
Коэффициент вычисляют по эмпирической формуле

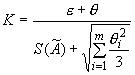
6. ФОРМА ЗАПИСИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

6.1. Оформление результатов измерений - по ГОСТ 8.011-72.

При симметричной доверительной погрешности результаты измерений представляют в форме

,

где - результат измерения.

Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности .

6.2. При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме

.

В случае, если границы неисключенной систематической погрешности вычислены в соответствии с п. 4.3, следует дополнительно указывать доверительную вероятность .

Примечания:

1. Оценка и могут быть выражены в абсолютной и относительной формах.

2. Определения терминов, встречающихся в стандарте, даны в справочном приложении 3.

ПРИЛОЖЕНИЕ 1 Справочное ПРОВЕРКА НОРМАЛЬНОСТИ РАСПРЕДЕЛЕНИЯ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ ГРУППЫ

ПРИЛОЖЕНИЕ 1
Справочное

При числе результатов наблюдений <50 нормальность их распределения проверяют при помощи составного критерия.

Критерий 1. Вычисляют отношение

,

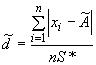где - смещенная оценка среднего квадратического отклонения, вычисляемая по формуле

.

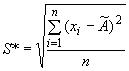Результаты наблюдений группы можно считать распределенными нормально, если

,

где и - квантили распределения, получаемые из табл. 1 по , и (1-), причем - заранее выбранный уровень значимости критерия.

Таблица 1

Статистика

	100%		(1-) 100%
	1%	5%	95%	99%
16	0,9137	0,8884	0,7236	0,6829
21	0,9001	0,8768	0,7304	0,6950
26	0,8901	0,8686	0,7360	0,7040
31	0,8826	0,8625	0,7404	0,7110
36	0,8769	0,8578	0,7440	0,7167
41	0,8722	0,8540	0,7470	0,7216
46	0,8682	0,8508	0,7496	0,7256
51	0,8648	0,8481	0,7518	0,7291

Критерий 2. Можно считать, что результаты наблюдений принадлежат нормальному распределению, если не более разностей превзошли значение ,

где - оценка среднего квадратического отклонения, вычисляемая по формуле

,

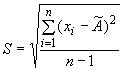где - верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности .

Значения определяются из табл. 2 по выбранному уровню значимости и числу результатов наблюдений .

При уровне значимости, отличном от предусмотренных в табл. 2, значение находят путем линейной интерполяции.

В случае, если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уровень значимости , а для критерия 2-, то результирующий уровень значимости составного критерия .

В случае, если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Таблица 2

Значения для вычисления

		·100%
		1%	2%	5%
10	1	0,98	0,98	0,96
11-14	1	0,99	0,98	0,97
15-20	1	0,99	0,99	0,98
21-22	2	0,98	0,97	0,96
23	2	0,98	0,98	0,96
24-27	2	0,98	0,98	0,97
28-32	2	0,99	0,98	0,97
33-35	2	0,99	0,98	0,98
36-49	2	0,99	0,99	0,98

ПРИЛОЖЕНИЕ 2 (Справочное) Значение коэффициента t для случайной величины Y, имеющей распределение Стьюдента с n-1 степенями свободы

ПРИЛОЖЕНИЕ 2
Справочное

Значение коэффициента для случайной величины , имеющей распределение Стьюдента с -1 степенями свободы

-1	=0,95	=0,99
3	3,182	5,841
4	2,776	4,604
5	2,571	4,032
6	2,447	3,707
7	2,365	3,499
8	2,306	3,355
9	2,262	3,250
10	2,228	3,169
12	2,179	3,055
14	2,145	2,977
16	2,120	2,921
18	2,101	2,878
20	2,086	2,845
22	2,074	2,819
24	2,064	2,797
26	2,056	2,779
28	2,048	2,763
30	2,043	2,750
	1,960	2,576

ПРИЛОЖЕНИЕ 3 (Справочное) ТЕРМИНЫ, ВСТРЕЧАЮЩИЕСЯ В СТАНДАРТЕ, И ИХ ОПРЕДЕЛЕНИЯ

ПРИЛОЖЕНИЕ 3
Справочное

Неисправленный результат наблюдения - результат наблюдения до введения поправок с целью устранения систематических погрешностей.

Исправленный результат наблюдения - результат наблюдения, получаемый после внесения поправок в неисправленный результат наблюдения.

Неисправленный результат измерения - среднее арифметическое результатов наблюдений до введения поправок с целью устранения систематических погрешностей.

Исправленный результат измерений - результат измерения, получаемый после внесения поправок в неисправленный результат измерения.

Группа результатов наблюдений - совокупность результатов наблюдений, полученная при условиях, которые в соответствии с целью измерения необходимы для получения результата измерения с заданной точностью.

Исключенная систематическая погрешность результата измерения - систематическая погрешность, которая остается неустраненной из результата измерения.