ГОСТ 25645.126-85
Поле геомагнитное. Модель поля внутриземных источников

ГОСТ 25645.126-85

Группа Т27

     
     
ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

ПОЛЕ ГЕОМАГНИТНОЕ

Модель поля внутриземных источников

Geomagnetic field.
Magnetic field model of internal originals

ОКСТУ 0080

Дата введения 1987-01-01

     
     
ИНФОРМАЦИОННЫЕ ДАННЫЕ

1. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 14.11.85 N 3609

ИСПОЛНИТЕЛИ

И.И.Алексеев, канд. физ.-мат. наук; А.В.Баюков, канд. техн. наук; Е.С.Беленькая, канд. физ.-мат. наук; Н.П.Бенькова, д-р физ.-мат. наук; Ю.А.Винтенко, канд. техн. наук; В.П.Головков, д-р физ.-мат. наук; Е.В.Горчаков, д-р физ.-мат. наук; М.С.Григорян; И.П.Иваненко, д-р физ.-мат. наук; В.В.Калегаев; Г.И.Коломийцева, канд. физ.-мат. наук; А.П.Кропоткин, д-р физ.-мат. наук; Е.Н.Лесновский, канд. техн. наук; В.М.Ломакин, канд. техн. наук; Ю.Г.Лютов; В.В.Мигулин, член-кор. АН СССР; Л.И.Мирошниченко, канд. физ.-мат. наук; В.Н.Никитинский; И.Я.Ремизов, канд. техн. наук; В.И.Степакин, канд. техн. наук; Л.Н.Степанова; И.Б.Теплов, д-р физ.-мат. наук; М.В.Терновская, канд. физ.-мат. наук; В.В.Хаустов, канд. техн. наук

2. СОГЛАСОВАНО с Государственной службой стандартных справочных данных (протокол от 16.06.85 N 18)

3. Срок первой проверки - 1989 г., периодичность проверки - 5 лет

4. ВВЕДЕН ВПЕРВЫЕ

5. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ

Обозначение НТД, на который дана ссылка	Номер пункта
ГОСТ 25645.127-85	1.1

6. ПЕРЕИЗДАНИЕ (декабрь 1989 г.) с Изменением N 1, утвержденным в сентябре 1989 г. (ИУС 12-89)

7. Проверен в 1989 г.


Настоящий стандарт устанавливает модель геомагнитного поля внутриземных источников на расстоянии от 100 до 40000 км от поверхности Земли.

Стандарт предназначен для использования в расчетах при определении условий функционирования технических устройств в космическом пространстве.

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

1.1. Вектор индукции магнитного поля в магнитосфере Земли вычисляют по формуле

, нТл, (1)

где - вектор индукции геомагнитного поля внутриземных источников;

- вектор индукции магнитного поля магнитосферных токов по ГОСТ 25645.127-85.

1.2. Магнитное поле внутриземных источников состоит из поля электрических токов в земном ядре (далее - главное поле), составляющего ~98% всего поля, и поля земной коры, являющегося полем магнетизма горных пород и составляющего ~2% всего поля.

Поле земной коры убывает с высотой быстрее, чем главное поле, и, начиная с высоты 100 км над земной поверхностью, им практически пренебрегают.

1.3. Модель главного поля представлена рядами сферических гармоник в зависимости от географических координат. При длине ряда 10-13 гармоник погрешность вычисления геомагнитного поля на поверхности Земли составляет 2%.

В первом приближении геомагнитное поле является полем диполя, расположенного в центре Земли, и представляется первым членом сферического гармонического ряда.

1.4. В связи с временными изменениями главного поля коэффициенты гармонических рядов периодически пересчитывают с учетом новых эмпирических данных. Изменения главного поля за один год (далее - вековой ход) также представлены рядами сферических гармоник.

2. МОДЕЛЬ ГЛАВНОГО ГЕОМАГНИТНОГО ПОЛЯ ВНУТРИЗЕМНЫХ ИСТОЧНИКОВ

2.1. Потенциал индукции геомагнитного поля внутриземных источников в точке пространства со сферическими координатами , , вычисляют по формуле

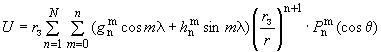, нТл·км, (2)

где полюс сферической системы координат совпадает с географическим полюсом Земли;

- геоцентрическое расстояние, км;

- долгота от Гринвичского меридиана, ...°;

- дополнение до широты, , ...°;

- широта в сферических координатах, ...°;

- средний радиус Земли, км;

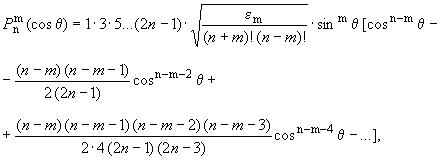(3)

где - нормировочный множитель,

2 для 1 и 1;

, - сферические гармонические коэффициенты, нТл;

- степень сферических гармоник;

- порядок сферических гармоник;

10 - максимальная степень сферических гармони

2.2. Все экспериментальные данные и положения ИСЗ в пространстве представляют в географических (геодезических) координатах , , , основанных на аппроксимации поверхности Земли эллипсоидом вращения. В ряде задач в первом приближении эллиптичностью Земли пренебрегают, не делая разницы между сферическими и геодезическими координатами. Однако при более точных расчетах необходимо учитывать сжатие Земли. Для учета сжатия Земли и вычисляют по формулам:

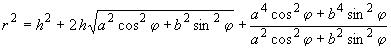, (4)

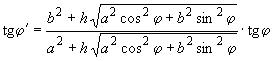, (5)

где - географическая (геодезическая) широта точки в пространстве, ...°;

- высота точки над уровнем моря, км;

- большая полуось земного эллипсоида вращения, км;

- малая полуось земного эллипсоида вращения, км.

Долготы в сферических и геодезических координатах тождественны.

Примечание. Значения и приведены в рекомендуемом приложении 1.

2.3. Составляющие вектора индукции геомагнитного поля внутриземных источников : , и вычисляют по формулам:

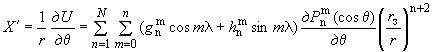, нТл, (6)

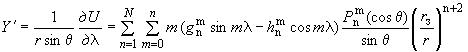, нТл, (7)

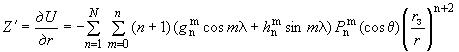, нТл. (8)

Составляющие , и используют для расчета вектора индукции по формуле (1).

(Измененная редакция, Изм. N 1).

2.4. Пространственно-временное распределение вектора индукции геомагнитного поля обычно описывают геомагнитными элементами:

прямоугольными составляющими , , , , нТл;

угловыми элементами и , ...°;

модулем вектора индукции , нТл.

Определения геомагнитных элементов приведены в приложении 2

2.4.1. В точке пространства с координатами , , прямоугольные составляющие вектора индукции в геодезической системе координат рассчитывают по формулам:

; (9)

, (10)

; (11)

. (12)

(Измененная редакция, Изм. N 1).

2.4.2. Угловые элементы и модуль вектора индукции вычисляют по формулам:

; (13)

; (14)

. (15)

2.4.3. Значения элемента поля для точки пространства при 0 получают линейной интерполяцией.

2.4.4. Значения сферических гармонических коэффициентов , для 1985 г. приведены в приложении 1, а результаты расчета поля на тот же год - в приложении 3.

Расчет поля на другие годы осуществляют с помощью векового хода. Пример программы для расчета геомагнитных элементов приведен в приложении 4.

(Измененная редакция, Изм. N 1).

2.5. Вековой ход геомагнитного поля определяют потенциалом , который вычисляют по формуле

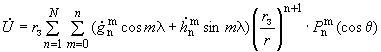, нТл км/год, (16)

где , - сферические гармонические коэффициенты, нТл/год.

2.5.1. При расчетах векового хода не учитывают сжатие Земли и пренебрегают различием между сферическими и задаваемыми географическими координатами (полагают , ).

2.5.2. Вековой ход элементов геомагнитного поля рассчитывают по формулам:

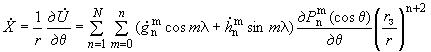, нТл/год, (17)

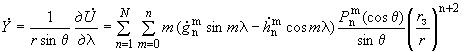, нТл/год, (18)

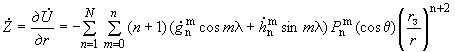, нТл/год, (19)

, нТл/год, (20)

, ...'/год, (21)

, ...'/год, (22)

, нТл/год, (23)

где элементы поля , , , , , , вычисляют по формулам (9-15);

при 0 определяют линейной интерполяцией.

2.5.3. Сферические гармонические коэффициенты , определяют по экспериментальным данным для различных временных интервалов. Значения , для 1985-1990 гг. приведены в приложении 5. Пример расчета векового хода приведен в приложении 3.

(Измененная редакция, Изм. N 1).

2.6. Главное поле на любой заданный год вычисляют способами, приведенными в пп.2.6.1 и 2.6.2.

2.6.1. Геомагнитные элементы на заданный год вычисляют по формуле

, (24)

где - любой из элементов поля (, , , , , и ) на год ;

- элемент поля, рассчитанный по , (известным на год ) по формулам (6-15) с учетом формул (4-5);

- вековой ход элемента поля, рассчитанный по , по формулам (17-23)

2.6.2. вычисляют по формулам (6-15), в которых , заменяют на

; (25)

*. (26)

________________
* Формула соответствует оригиналу. - Примечание изготовителя базы данных.

2.6.3. Для составляющих , , расчеты обоими способами дают тождественные результаты. Для остальных элементов расхождения лежат в пределах погрешностей. Выбор способа определяется условиями поставленных задач.

2.6.4. Пример расчета на 1989 г. по п.2.6.2 дан в программе, приведенной в приложении 4.

2.6.5. Примеры расчета поля на 1988 г. обоими способами приведены в приложении 3.

2.6.4, 2.6.5. (Измененная редакция, Изм. N 1).

3. ПАРАМЕТРЫ ГЕОМАГНИТНОГО ДИПОЛЯ

3.1. Дипольное геомагнитное поле соответствует полю, представленному первым членом сферических гармоник. Составляющие дипольного члена рассчитывают по формулам:

;

;

.

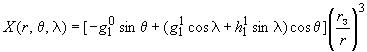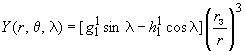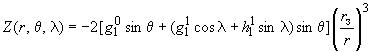3.2. Координаты полюсов дипольного поля (геомагнитных полюсов) и его магнитный момент рассчитывают по формулам:

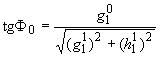, (27)

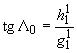, (28)

, Тл·м, (29)

где - географическая широта геомагнитного полюса, ...°;

- географическая долгота геомагнитного полюса, ...°.

3.3. Параметры геомагнитного диполя для 1985 г. приведены в приложении 6. Пример расчета дипольного поля приведен в приложении 3.

(Измененная редакция, Изм. N 1).

ПРИЛОЖЕНИЕ 1 (рекомендуемое). Сферические гармонические коэффициенты g_(m)(n), h_(m)(n), нТл, для 1985 г.

ПРИЛОЖЕНИЕ 1
Рекомендуемое

Сферические гармонические коэффициенты , , нТл, для 1985 г.

1	0	-29877	0
1	1	-1903	5497
2	0	-2073	0
2	1	3045	-2191
2	2	1691	-309
3	0	1300	0
3	1	-2208	-312
3	2	1244	284
3	3	835	-296
4	0	937	0
4	1	780	233
4	2	363	-250
4	3	-426	68
4	4	169	-298
5	0	-215	0
5	1	356	47
5	2	253	148
5	3	-94	-155
5	4	-161	-75
5	5	-48	95
6	0	52	0
6	1	65	-16
6	2	50	90
6	3	-186	69
6	4	4	-50
6	5	17	-4
6	6	-102	20
7	0	75	0
7	1	-61	-82
7	2	2	-26
7	3	24	-1
7	4	-6	23
7	5	4	17
7	6	9	-21
7	7	0	-6
8	0	21	0
8	1	6	7
8	2	0	-21
8	3	-11	5
8	4	-9	-25
8	5	2	11
8	6	4	12
8	7	4	-16
8	8	-6	-10
9	0	5	0
9	1	10	-21
9	2	1	16
9	3	-12	9
9	4	9	-5
9	5	-3	-6
9	6	-1	9
9	7	7	10
9	8	2	-6
9	9	-5	2
10	0	-4	0
10	1	-4	1
10	2	2	0
10	3	-5	3
10	4	-2	6
10	5	5	-4
10	6	3	0
10	7	1	-1
10	8	2	4
10	9	3	0
10	10	0	-6

Примечание. Длина аппроксимирующего ряда 10.

Коэффициенты и соответствуют значениям параметров фигуры Земли:

6371,2 км;

6378,2 км;

6356,8 км.

(Измененная редакция, Изм. N 1).

ПРИЛОЖЕНИЕ 2 (cправочное). ОПРЕДЕЛЕНИЯ ГЕОМАГНИТНЫХ ЭЛЕМЕНТОВ И ПОЯСНЕНИЯ К НИМ

ПРИЛОЖЕНИЕ 2
Справочное

- северная составляющая вектора индукции - проекция вектора на ось , направленную по географическому меридиану (на север).

- восточная составляющая вектора индукции - проекция на ось , направленную по параллели (на восток).

- вертикальная составляющая вектора индукции - проекция на ось , направленную вертикально вниз.

- горизонтальная составляющая вектора индукции - проекция на горизонтальную плоскость .

- магнитное склонение - угол между географическим и магнитным меридианами (положительное к востоку).

- магнитное наклонение - угол между горизонтальной плоскостью и направлением вектора (положительное при направлении вектора вниз).

- модуль вектора .

ПРИЛОЖЕНИЕ 3 (справочное). ПРИМЕРЫ РАСЧЕТОВ ЭЛЕМЕНТОВ ПОЛЯ И ВЕКОВОГО ХОДА

ПРИЛОЖЕНИЕ 3
Справочное

     
ПРИМЕРЫ РАСЧЕТОВ ЭЛЕМЕНТОВ ПОЛЯ И ВЕКОВОГО ХОДА
СОСТАВЛЯЮЩИЕ , , И ЭЛЕМЕНТЫ ПОЛЯ , , , , , нТл;
 , В ГРАДУСАХ ВЕКОВОЙ ХОД , , , , , нТл/год; , , мин/год

Таблица 1

1. Пример расчета геомагнитного поля на 1985 г. по формулам (4-15)

1.1. Главное поле
100,0	80,6	58,0	6457,4	80,6	4574,9	2437,6	53981,6	4632,7	2437,6	53976,7
3000,0	80,6	58,0	9357,4	80,6	2126,7	-151,6	18665,3	2140,5	-151,6	18663,8
6385,0	80,6	58,0	12742,4	80,6	944,5	-202,8	7447,0	948,5	-202,8	7446,5
12742,4	80,6	58,0	19099,8	80,6	300,6	-94,3	2203,3	301,4	-94,3	2203,1
40000,0	80,6	58,0	46357,3	80,6	21,9	-9,5	152,0	21,9	-9,5	152,0
1.2. Дипольное поле (1)
100,0	80,6	58,0	6457,4	80,6	8178,5	-4348,0	55459,8	8237,8	-4348,0	55451,0
3000,0	80,6	58,0	9357,4	80,6	2684,7	-1428,9	18227,4	2698,1	-1428,9	18225,4
6971,2	80,6	58,0	12748,6	80,6	1065,9	-567,7	7242,2	1069,8	-567,7	7241,7
12742,4	80,6	58,0	19099,8	80,6	315,3	-168,0	2143,6	316,1	-168,0	2143,5
40000,0	80,6	58,0	46357,3	80,6	22,0	-11,8	149,9	22,1	-11,8	149,9

Таблица 2

2. Пример расчета геомагнитного поля на 1985 г. без учета эллиптичности Земли по формулам (6-15)

2.1. Главное поле
100,0	80,6	58,0	6471,2	4542,2	2385,8	53667,5	53912,2	5130,6	27,7	84,5
3000,0	80,6	58,0	9371,2	2112,8	-154,1	18586,5	18706,8	2118,5	-4,2	83,5
6371,2	80,6	58,0	12742,4	942,5	-202,9	7447,8	7509,9	964,1	-12,1	82,6
12742,4	80,6	58,0	19113,6	299,5	-94,1	2198,6	2220,9	314,0	-17,4	81,9
40000,0	80,6	58,0	46371,2	21,9	-9,5	151,9	153,7	23,9	-23,4	81,1
2.2. Дипольное поле
6371,2	80,6	58,0	12742,4	1060,5	-565,8	7219,8	7319,2	1202,0	-28,1	80,5
12742,4	80,6	58,0	19113,6	314,2	-167,7	2139,2	2168,6	356,1	-28,1	80,5

Таблица 3

3. Пример расчета векового хода по формулам (17-23)

100,0	80,6	58,0	-31,0	2,5	-27,4	-29,7	-26,3	11,2	1,5
3000,0	80,6	58,0	-7,8	5,9	-4,9	-5,8	-8,2	8,6	1,4
6385,0	80,6	58,0	-2,8	2,8	-2,1	-2,6	-3,3	7,6	1,4
12742,4	80,6	58,0	-0,7	0,9	-0,8	-0,9	-1,0	6,5	1,3
40000,0	80,6	58,0	0,0	0,1	-0,1	-0,1	-0,1	5,1	1,1
100,0	0,0	0,0	-13,4	59,7	-59,3	5,4	-22,8	7,3	-7,3
3000,0	0,0	0,0	-5,7	15,8	-13,3	-5,6	-8,4	5,8	-5,7
6385,0	0,0	0,0	-2,4	5,1	-4,5	-2,9	-3,3	4,5	-4,6
12742,4	0,0	0,0	-0,7	1,2	-1,1	-1,0	-0,9	3,4	-3,7
40000,0	0,0	0,0	-0,1	0,1	-0,1	-0,1	-0,1	2,3	-2,8

Таблица 4

4. Пример расчета главного поля на 1988 г.

4.1. По формуле (24)
100,0	80,6	58,0	4539,7	2445,1	53894,5	54140,8	5155,9	28,36	84,6
3000,0	80,6	58,0	2117,1	-133,9	18649,1	18769,3	2121,3	-3,67	83,5
100,0	0,0	0,0	26204,2	-4086,1	-13066,1	20563,9	26520,3	-8,84	-26,3
3000,0	0,0	0,0	8495,2	-1476,3	-1706,9	8809,5	8622,4	-9,81	-11,8
4.2. По формулам (25, 26)
100,0	80,6	58,0	4538,4	2444,6	53893,9	54139,8	5154,9	28,3	84,5
3000,0	80,6	58,0	2117,0	-133,8	18649,0	18769,3	2121,2	-3,6	83,5
100,0	0,0	0,0	26204,2	-4086,6	-13065,1	29564,4	26520,9	-8,9	-26,2
3000,0	0,0	0,0	8495,2	-1476,4	-1806,9	8809,8	8622,5	-9,9	-11,8

(Измененная редакция, Изм. N 1).

ПРИЛОЖЕНИЕ 4 (справочное)

ПРИЛОЖЕНИЕ 4
Справочное

	С		ПРОГРАММА РАСЧЕТА ГЕОМАГНИТНОГО ПОЛЯ "В1"
	С		НА ЗАДАННЫЙ ГОД "Т"
	С
	С
0001			INTEGER E,YEAR,YEAR1
0002			REAL L,L1,LP,NR
0003			DIMENSION P(17,17),R(17,17),G(150),G1(150),DG(150),
			·DG1(150),U1(17),U2(17),S(17,17),H1(400),F1(400),L(400)
	С
	С			СЧИТЫВАНИЕ МАССИВА ДАННЫХ
0004			DATA NH/10/,E/1/,KT/6/
	С			NH=ЧИСЛО ГАРМОНИК
	С			Е - УЧЕТ ЭЛЛИПТИЧНОСТИ:
	С			Е=1 - УЧИТЫВАЕТСЯ, Е=0 - НЕ УЧИТЫВАЕТСЯ
	С			КТ - КОЛИЧЕСТВО ТОЧЕК
0005			DATA YEAR/1989/
	С			YEAR - ЗАДАННЫЙ ГОД (Т)
0006			K=(NH·NH+3·NH)/2
	С			К - КОЛИЧЕСТВО КОЭФФИЦИЕНТОВ
	С	G(I) - КОЭФФИЦИЕНТЫ G, ЗАДАННЫЕ НА 1985 Г.,
	С			В НАНОТЕСЛАХ
0007			DATA G/-29877.,-1903,-2073.,3045.,1691.,1300.,
			·-2208.,1244.,835.,937.,780.,363.,-426.,169.,
			·-215.,356.,253.,-94.,-161.,-48.,52.,65.,50.,
			·-186.,4.,17.,-102.,75.,-61.,2.,24.,-6.,4.,9.,
			·0.,21.,6.,0.,-11.,-9.,2.,4.,4.,-6.,5.,10.,1.,
			·-12.,9.,-3.,-1.,7.,2.,-5.,-4.,-4.,2.,-5.,-2.,
			·5.,3.,1.,2.,3.,0./
	С	G1(I) - КОЭФФИЦИЕНТЫ Н, ЗАДАННЫЕ НА 1985 Г.,
	С		В НАНОТЕСЛАХ
0008			DATA G1/0.,5497.,0.,-2191.,-309.,0.,-312.,284.,
			·-296.,0.,233.,-250.,68.,-298.,0.,47.,148.,
			·-155.,-75.,95.,0.,-16.,90.,69.,-50.,-4.,20.,0.,
			·-82.,-26.,-1.,23.,17.,-21.,-6.,0.,7.,-21.,5.,
			·-25.,11.,12.,-16.,-10.,0.,-21.,16.,9.,-5.,-6.,
			·9.,10.,-6.,2.,0.,1.,0.,3.,6.,-4.,0.,-1.,4.,0.,-6./
	С	DG(I) - КОЭФФИЦИЕНТЫ DG, ЗАДАННЫЕ НА 1985 Г.,
	С		В НАНОТЕСЛАХ/ГОД
0009			DATA DG/19.7,11.5,-12.6,1.8,1.4,4.3,-6.1,-0,7,
			·-3.8,-0.4,0.2,-7.4,-0.4,-5.7,1.2,-0.1,-1.2,
			·-2.4,-0.3,0.5,1.4,-0.4,1.6,0.9,-0.1,0.7,1.0,
			·0.4,-0.6,-0.1,0.2,0.9,0.9,0.3,1.0,0.5,-0.3,
			·-0.1,0.6,-0.7,0.1,0.2,-0.9,-0.5,21·0./
	С	DG1(I) - КОЭФФИЦИЕНТЫ DH, ЗАДАННЫЕ НА 1985 Г.,
	С		В НАНОТЕСЛАХ/ГОД
0010			DATA DG1/0.,-20.,0.,-16.4,-15.9,0.,4.6,2.8,
			·-9.8,0.,3.5,2.,3.7,-0.3,0.,0.,0.7,0.1,1.1,-0.1,
			·0.,-0.7,-1.2,-0.3,-1.3,0.4,1.1,0.,1.,0.3,0.8,
			·0.7,-0.2,0.3,0.,0.,0.6,-0.3,0.4,0.,0.6,-1.2,
			·-0.1,0.8,21·0./
	С	Н1(I) - ВЫСОТА ТОЧКИ В КM
0011			DATA H1/100.,3000.,6371.2,6385.,12742.4,40000./
	С	F1(I) - ШИРОТА ТОЧКИ В ГРАД.
0012			DATA F1/6·80.6/
	С	L(I) - ДОЛГОТА ТОЧКИ В ГРАД.
0013			DATA L/6·58.0/
0014			PRINT 12
0015		12	FORMAT('1',//10X,'G(I) - МАССИВ КОЭФФИЦИЕНТОВ',
			·'G ДЛЯ 1985 Г.:'/)
0016			PRINT 9,(G(I),I=1,K)
0017			PRINT 13
0018		13	FORMAT(//10X,'G1(I) - МАССИВ КОЭФФИЦИЕНТОВ Н',
			·'ДЛЯ 1985 Г.:'/)
0019			PRINT 9,(G1(I),I=1,K)
0020			PRINT 14
0021		14	FORMAT (//5X,'DG(I) - МАССИВ КОЭФФИЦИЕНТОВ G0',
			·'ДЛЯ ИНТЕРВАЛА 1985-1990 ГГ.,:'/)
0022			PRINT 9,(DG(I),I=1,K)
0023			PRINT 15
0024		15	FORMAT (//5X,'DG1(I) - МАССИВ КОЭФФИЦИЕНТОВ Н0',
			·'ДЛЯ ИНТЕРВАЛА 1985-1990 ГГ.,:'/)
0025			PRINT 9,(DG1(I),I=1,K)
	С
	С		РАСЧЕТ КОЭФФИЦИЕНТОВ 'G' И 'H' НА ГОД 'Т'
0026			DO 11 I=1,K
0027			YEAR1=YEAR-1985
0028			G(I)=G(I)+DG(I)·YEAR1
0029		11	G1(I)=G1(I)+DG1(I)-YEAR1
0030			PRINT 55
0031		55	FORMAT ('1',20Х,'РЕЗУЛЬТАТЫ',
			·'PACЧETA'///)
0032			PRINT 8
0033		8	FORMAT (//5X,'GT - МАССИВ КОЭФФИЦИЕНТОВ G,',
			·'РАССЧИТАННЫХ НА 1989 Г.:'/)
0034			PRINT 9,(G(I),I=1,K)
0035		9	FORMAT(4E18.6)
0036			PRINT 10
0037		10	FORMAT (//5X,'HT - МАССИВ КОЭФФИЦИЕНТОВ Н,',
			·'РАССЧИТАННЫХ НА 1989 Г.:'/)
0038			PRINT 9,(G1(I),I=I,K)
	С
	С			РАСЧЕТ ЭЛЕМЕНТОВ ПОЛЯ
0039			IF(PR.EQ.0) GOTO 18
0041		18	PI=3.141593
0042			RS=6371.2
	С			RS - СРЕДНИЙ РАДИУС ЗЕМЛИ
0043			A =6378.2
0044			В =6356.8
0045			А3=.1Е-7
0046			NH=NH+1
0047			I=0
0048			IK=0
0049			IN=1
0050			PRINT 19,IN
0051		19	FORMAT (//10Х,'IN=',13)
0052		20	I=I+1
0053			F2=F1(I)-PI/180.
0054			IF(E.EQ.0) GOTO 21
0056			S1=A··2·COS(F2)··2+B··2·SIN(F2)··2
0057			S2=A··4·COS(F2)··2+B··4·SIN(F2)··2
0058			R1=SQRT(H1(I)··2+2·H1(I)·SQRT(S1)+S2/S1)
0059			ARG=(B··2+H1(I)·SQRT(S1))/(A··2+H1(I)·SQRT(S1))·
			·(SIN(F2)/COS(F2))
0060			F3=ATAN(ARG)
0061			F2=F2-F3
0062			S1=SIN(F2)
0063			S2=COS(F2)
0064			GOTO 22
0065		21	F3=F2
0066		22	F=PI/2.-F3
0067			C1=SIN(F)
0068			C2=COS(F)
0069			S(1,1)=1.
0070			DO 24 N=2,NH
0071			S(1,N)=S(1,N-1)·(2·N-3.)/(N-1)
0072			S(2,N)=S(1,N)·SQRT((N-1.)·2/N)
0073			IF(N.LT.3) GOTO 24
0075			DO 23 M=3,N
0076		23	S(M,N)=S(M-1,N)·SQRT((N-M+1.)/(N+M-2.))
0077		24	CONTINUE
0078			P(1,1)=1.
0079			R(1,1)=0.
0080			P(1,2)=C2
0081			R(1,2)=-C1
0082			P(2,2)=C1
0083			R(2,2)=C2
0084			DO 28 N=3,NH
0085			DO 28 M=1,N
0086			IF(M-N) 27,26,25
0087		25	P(M,N)=0.
0088			R(M,N)=0.
0089			GOTO 28
0090		26	P(M,N)=C1·P(M-1,N-1)
0091			R(M,N)=C1·R(M-1,N-1)+C2·P(M-1,N-1)
0092			GOTO 28
0093		27	NR=((N-2.)··2-(M-1.)··2)/((2·N-3.)·(2·N-5.))
0094			P(M,N)=C2·P(M,N-1)-NR·P(M,N-2)
0095			R(M,N)=C2·R(M,N-1)-C1·P(M,N-1)-NR·R(M,N-2)
0096		28	CONTINUE
0097			DO 29 N=1,NH
0098			DO 29 M=1,N
0099			P(M,N)=P(M,N)·S(M,N)
0100		29	R(M,N)=R(M,N)·S(M,N)
0101			L(I)=L(I)·PI/180.
0102			DO 30 M=1,NH
0103			U1(M)=SIN((M-1)·L(I))
0104		30	U2(M)=COS((M-1)·L(I))
0105			IF(E.EQ.1) GOTO 31
0107			L1=RS/(RS+H1(I))
0108			GOTO 32
0109		31	L1=RS/R1
0110		32	A1=ABS(SIN(F))
0111			IF(A1.LT.A3) GOTO 33
0113			A1=SIN(F)
0114			GOTO 34
0115		33	А1=А3
0116		34	Х=0.
0117			Y=0.
0118			Z=0.
0119			J=0.
0120			DO 35 N=2,NH
0121			DO 35 M=1,N
0122			A2=(M-1)/A1
0123			J=J+1
0124			X=X+(G(J)·U2(M)+G1(J)·U1(M))·L1··(N+1)·R(M,N)
0125			Y=Y+(G(J)·U1(M)-G1(J)·U2(M))·L1··(N+1)·P(M,N)·A2
0126		35	Z=Z+(-1)·N·(G(J)·U2(M)+G1(J)·U1(M))·L1··(N+1)·P(M,N)
0127			IF(E.EQ.0.) GOTO 36
0129			Х1=Х·S2+Z·S1
0130			Z1=Z·S2-X·S1
0131			X=Х1
0132			Z=Z1
0133		36	T=SQRT(X··2+Y··2+Z··2)
0134			HC=SQRT(X··2+Y··2)
0135			D=ATAN(Y/X)
0136			IF(Y) 38,37,37
0137		37	IF(X) 40,41,41
0138		38	IF(X) 40,39,39
0139		39	D=2.·PI+D
0140			GOTO 41
0141		40	D=PI+D
0142		41	LP=ATAN(Z/HC)
0143			IF(D-PI) 43,42,42
0144		42	D=D-2.·PI
0145		43	L(I)=L(I)/.01745329
0146			LP=LP/.01745329
0147			D=D/.01745329
0148			IF(I.EQ.1) GOTO 44
0150			IF(I.EQ.IK+68) GOTO 48
0152			GOTO 66
0153		44	PRINT 63
0154		63	FORMAT (//4X,'H1',5X,'F',5X,'L',6X,'X',7X,'Y',7X,
			·'Z',7X,'T',7X,'H',6X,'D',5Х,'I'//)
0155		64	FORMAT(F8.1,2F6.1,5F8.1,2F6.1)
0156		66	PRINT 64,H1(I),F1(I),L(I),X,Y,Z,T,HC,D,LP
0157			GOTO 49
0158		48	IK=IK+67
0159			IN=IN+1
0160			PRINT 19,IN
0161			GOTO 44
0162		49	IF(I.LT.KT) GOTO 20
0164			STOP
0165			END

РЕЗУЛЬТАТЫ РАСЧЕТА

GT - МАССИВ КОЭФФИЦИЕНТОВ G, РАССЧИТАННЫХ НА 1989 Г.:

-0.297982Е+05	-0.185700Е+04	-0.212340Е+04	0.305220Е+04
0.169660Е+04	0.131720E+04	-0.223240Е+04	0.124120Е+04
0.819800Е+03	0.935400Е+03	0.780800Е+03	0.333400Е+03
-0.427600Е+03	0.146200Е+03	-0.210200Е+03	0.355600Е+03
0.248200Е+03	-0.103600Е+03	-0,162200Е+03	-0.460000Е+02
0.576000Е+02	0.634000Е+02	0.564000Е+02	-0.182400Е+03
0.360000Е+01	0.198000Е+02	-0.980000E+02	0.766000Е+02
-0.634000Е+02	0.160000Е+01	0.248000Е+02	-0.240000Е+01
0.760000Е+01	0.102000Е+02	0.400000Е+01	0.230000Е+02
0.480000Е+01	-0.400000Е+00	-0.860000Е+01	-0.118000Е+02
0.240000Е+01	0.480000Е+01	0.400000Е+00	-0.800000Е+01
0.500000Е+01	0.100000Е+02	0.100000Е+01	-0.120000Е+02
0.900000Е+01	-0.300000Е+01	-0.100000Е+01	0.700000Е+01
0.200000E+01	-0.500000Е+01	-0.400000Е+01	-0.400000Е+01
0.200000Е+01	-0.500000Е+01	-0.200000Е+01	0.500000Е+01
0.300000Е+01	0.100000Е+01	0.200000Е+01	0.300000Е+01
0.000000Е+00

НТ - МАССИВ КОЭФФИЦИЕНТОВ Н, РАССЧИТАННЫХ НА 1989 Г.:

0.000000Е+00	0.541700Е+04	0.000000Е+00	-0.225660Е+04
-0.372600Е+03	0.000000Е+00	-0.293600Е+03	0.295200Е+03
-0.335200Е+03	0.000000Е+00	0.247000Е+03	-0.242000E+03
0.828000Е+02	-0.299200E+03	0.000000Е+00	0.470000Е+02
0.150800Е+03	-0.154600Е+03	-0.706000Е+02	0.946000Е+02
0.000000Е+00	-0.188000Е+02	0.852000Е+02	0.678000Е+02
-0.552000Е+02	-0.240000Е+01	0.244000Е+02	0.000000Е+00
-0.780000Е+02	-0.248000Е+02	0.220000Е+01	0.258000Е+02
0.162000Е+02	-0.198000Е+02	-0.600000Е+01	0.000000Е+00
0.940000Е+01	-0.222000Е+02	0.660000Е+01	-0.250000Е+02
0.134000Е+02	0.720000Е+01	-0.164000Е+02	-0.680000Е+01
0.000000Е+00	-0.210000Е+02	0.160000Е+02	0.900000Е+01
-0.500000Е+01	-0.600000Е+01	0.900000Е+01	0.100000Е+02
-0.600000Е+01	0.200000Е+01	0.000000Е+00	0.100000Е+01
0.000000Е+00	0.300000Е+01	0.600000Е+01	-0.400000Е+01
0.000000Е+00	-0.100000Е+01	0.400000Е+01	0.000000Е+00
-0.600000Е+01

IN=	1
H1	F	L	X	Y	Z	Т	Н	D	I
100.0	80.6	58.0	4507.0	2446.9	53865.8	54109.4	5128.4	28.5	84.6
3000.0	80.6	58.0	2109.1	-127.9	18644.0	18763.3	2113.0	-3.5	83.5
6371.0	80.6	58.0	940.1	-191.9	7462.1	7523.5	959.4	-11.5	82.7
6385.0	80.6	58.0	937.3	-191.6	7437.9	7499.1	956.7	-11.6	82.7
12742.4	80.6	58.0	298.4	-90.8	2199.9	2221.9	311.9	-16.9	81.9
40000.0	80.6	58.0	21.8	-9.2	151.7	153.5	23.7	-23.0	81.1

КОММЕНТАРИИ

Входные данные:

NH=N=10;

Е=1 - признак учета эллиптичности Земли;

КТ=6 - количество точек с заданными координатами (, , );

YEAR - заданный год 1989;

G(I) - массив коэффициентов , заданных на год 1985;

G1(I) - массив коэффициентов , заданных на год 1985;

H1(I) - массив высот (км) заданного числа точек;

F1(I) - массив широт (в ...°) заданного числа точек;

L(I) - массив долгот (в ...°) заданного числа точек;

DG(I) - массив коэффициентов , заданных для 1985-1990 гг.;

DG1(I) - массив коэффициентов , данных для 1985-1990 гг.;

Выходные данные:

печать названия программы с указанием года 1989;

печать входных данных NH, Е, KT, а также рассчитанного в программе общего числа коэффициентов ;

массив G коэффициентов , заданных на год ;

массив Н коэффициентов , заданных на год ;

массив DG коэффициентов , заданных на интервал 1985-1990;

массив DH коэффициентов , заданных на интервал 1985-1990;

массив GT коэффициентов , рассчитанных на год ;

массив НТ коэффициентов , рассчитанных на год ;

H1 - высота (км) заданной точки пространства;

F - широта (...°) заданной точки пространства;

L - долгота (... °) заданной точки пространства;

X, Y, Z, Т, Н, D, I - значения элементов в заданной точке (, , ) на год 1989.

ПРИЛОЖЕНИЕ 5 (рекомендуемое). Сферические гармонические коэффициенты

ПРИЛОЖЕНИЕ 5
Рекомендуемое

     
Сферические гармонические коэффициенты , , нТл/год,
для интервала 1985-1990 гг.

1	0	19.7	0.0
1	1	11.5	-20.0
2	0	-12.6	0.0
2	1	1.8	-16.4
2	2	1.4	-15.9
3	0	4.3	0.0
3	1	-6.1	4.6
3	2	-0.7	2.8
3	3	-3.8	-9.8
4	0	-0.4	0.0
4	1	0.2	3.5
4	2	-7.4	2.0
4	3	-0.4	3.7
4	4	-5.7	-0.3
5	0	1.2	0.0
5	1	-0.1	0.0
5	2	-1.2	0.7
5	3	-2.4	0.1
5	4	-0.3	1.1
5	5	0.5	-0.1
6	0	1.4	0.0
6	1	-0.4	-0.7
6	2	1.6	-1.2
6	3	0.9	-0.3
6	4	-0.1	-1.3
6	5	0.7	0.4
6	6	1.0	1.1
7	0	0.4	0.0
7	1	-0.6	1.0
7	2	-0.1	0.3
7	3	0.2	0.8
7	4	0.9	0.7
7	5	0.9	-0.2
7	6	0.3	0.3
7	7	1.0	0.0
8	0	0.5	0.0
8	1	-0.3	0.6
8	2	-0.1	-0.3
8	3	0.6	0.4
8	4	-0.7	0.0
8	5	0.1	0.6
8	6	0.2	-1.2
8	7	-0.9	-0.1
8	8	-0.5	0.8

Примечание. Длина аппроксимирующего ряда 8.

ПРИЛОЖЕНИЕ 6 (рекомендуемое)

ПРИЛОЖЕНИЕ 6
Рекомендуемое

Параметры геомагнитного диполя на 1985 г.:

7,87·10 Тл·м.

Географические координаты северного геомагнитного полюса:

79,0° северной широты,

289,1° восточной долготы.

Приложения 3-6. (Измененная редакция, Изм. N 1).