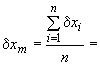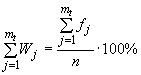ГОСТ 23615-79
Группа Ж02
МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
Система обеспечения точности геометрических параметров в строительстве
СТАТИСТИЧЕСКИЙ АНАЛИЗ ТОЧНОСТИ
System for ensuring the accuracy of geometrical parameters in construction. Statistical analysis of accuracy
МКС 01.100.30
91.010.30
Дата введения 1980-01-01
Постановлением Государственного комитета СССР по делам строительства от 12 апреля 1979 г. N 55 дата введения установлена 01.01.80
ИЗДАНИЕ (апрель 2003 г.) с Изменением N 1, утвержденным в июне 1986 г. (ИУС 11-86).
Настоящий стандарт устанавливает общие правила статистического анализа точности геометрических параметров при изготовлении строительных элементов (деталей, изделий, конструкций), выполнении разбивочных работ в процессе строительства и установке элементов в конструкциях зданий и сооружений.
Стандарт распространяется на технологические процессы и операции массового и серийного производства.
Применяемые в стандарте термины по статистическому анализу и контролю соответствуют приведенным в ГОСТ 15895-77*.
________________
* На территории Российской Федерации действуют ГОСТ Р 50779.10-2000, ГОСТ Р 50779.11-2000.
Стандарт полностью соответствует СТ СЭВ 5061-85.
(Измененная редакция, Изм. N 1).
1. ОБЩИЕ ПОЛОЖЕНИЯ
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Статистическим анализом устанавливают закономерность распределения действительных значений геометрических параметров конструкций зданий и сооружений и их элементов и определяют статистические характеристики точности этих параметров.
1.2. На основе результатов статистического анализа:
производят оценку действительной точности и устанавливают возможности технологических процессов и операций по ее обеспечению;
определяют возможность применения статистических методов регулирования точности по СТ СЭВ 2835-80 и контроля точности по ГОСТ 23616-79;
проверяют эффективность применяемых методов регулирования и контроля точности при управлении технологическими процессами.
1.3. Статистический анализ точности выполняют отдельно по каждому геометрическому параметру в следующей последовательности:
в зависимости от характера производства образуют необходимые выборки и определяют действительные отклонения параметра от номинального;
рассчитывают статистические характеристики действительной точности параметра в выборках;
проверяют статистическую однородность процесса - согласие опытного распределения действительных отклонений параметра с теоретическим и стабильность статистических характеристик в выборках;
оценивают точность технологического процесса и, в зависимости от цели анализа, принимают решение о порядке применения его результатов.
1.4. Статистический анализ точности следует проводить после предварительного изучения состояния технологического процесса в соответствии с требованиями СТ СЭВ 2835-80 и его наладки по полученным результатам.
1.5. Действительные отклонения геометрического параметра в выборках определяют в результате его измерений в соответствии с требованиями ГОСТ 23616-79 и ГОСТ 26433.0-85.
1.2-1.5 (Измененная редакция, Изм. N 1).
2. ОБРАЗОВАНИЕ ВЫБОРОК
2.1. В качестве исследуемой генеральной совокупности принимают объем продукции или работ (например, разбивочных), производимый на технологической линии (потоке, участке и т.п.) при неизменных типовых условиях производства в течение определенного времени, достаточного для характеристики данного процесса.
2.2. Статистический анализ точности выполняют по действительным отклонениям параметра в представительной объединенной выборке, состоящей из не менее чем 100 объектов контроля и получаемой путем последовательного отбора из исследуемой совокупности серии выборок малого объема.
Эти выборки отбирают через равные промежутки времени, определяемые в зависимости от объема производства и особенностей технологического процесса.
(Измененная редакция, Изм. N 1).
2.3. При анализе точности процессов изготовления элементов массового производства, когда на каждой единице или комплекте технологического оборудования постоянно в достаточно большом объеме производится однотипная продукция (например, кирпич, асбестоцементные листы), отбирают серию мгновенных выборок одинакового объема 
5
10 единицам.
2.4. При анализе точности изготовления элементов серийного производства, когда достаточный объем продукции может быть получен с нескольких однотипных единиц технологического оборудования (например, производство железобетонных изделий ряда видов, сборка металлоконструкций и т.п.), отбирают серию выборок одинакового объема 
30 единицам. Эти выборки могут быть составлены из изделий, отбираемых при приемочном контроле нескольких последовательных или параллельных партий продукции.
2.5. При анализе точности разбивки осей и установки элементов образуют серию выборок одинакового объема из 30 закрепленных в натуре ориентиров или элементов, установленных на одном или нескольких монтажных горизонтах.
2.4, 2.5 (Измененная редакция, Изм. N 1).
2.6. Порядок формирования выборки для обеспечения ее представительности и случайности определяют в соответствии с характером объекта исследований и требованиями ГОСТ 18321-73.
3. РАСЧЕТ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ТОЧНОСТИ
3.1. При проведении статистического анализа вычисляют выборочные средние отклонения, а также выборочные среднеквадратичные отклонения или размахи действительных отклонений в выборках.
Примечание. При анализе точности конфигурации элементов выборочные средние отклонения не вычисляют.
3.2. Выборочное среднее отклонение 
в выборках малого объема и в объединенной выборке вычисляют по формуле
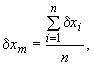(1)
где 
- действительное отклонение;
- объем выборки.
3.3. Выборочное среднеквадратичное отклонение 
в выборках малого объема 30 единицам и в объединенной выборке вычисляют по формуле
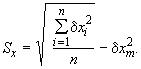(2)
В случаях, когда выборочное среднее отклонение в соответствии с примечанием к п.3.1 не вычисляют, значение в формуле (2) принимают равным нулю.
3.4. Размахи 
действительных отклонений параметра определяют в выборках малого объема из 510 единицам по формуле
(3)
где 
и 
- наибольшее и наименьшее значения 
в выборке.
3.1-3.4 (Измененная редакция, Изм. N 1).
3.5. Порядок расчета статистических характеристик приведен в приложении 1.
3.6. В качестве статистических характеристик точности процесса принимают значения и в объединенной выборке, если результаты проведенной в соответствии с разд.4 проверки подтвердили статистическую однородность процесса.
Значения 
и в выборках малого объема используют при проверке однородности процесса.
(Измененная редакция, Изм. N 1).
4. ПРОВЕРКА СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ ПРОЦЕССА
4.1. При проверке статистической однородности процесса устанавливают:
согласие распределения действительных отклонений параметра в объединенной выборке с теоретическим;
стабильность выборочного среднего отклонения , значение которого характеризует систематические погрешности прогресса;
стабильность выборочного среднеквадратичного отклонения или размаха , значения которых характеризуют случайные погрешности прогресса.
4.2. Согласие распределения действительных отклонений параметра с теоретическим устанавливают по нормативно-технической документации.
Допускается использование других методов, принятых в математической статистике (например, построение ряда отклонений на вероятностной бумаге и т.д.).
4.3. При нормальном распределении геометрического параметра стабильность статистических характеристик в мгновенных выборках и выборках малого объема 30 единицам проверяют по попаданию их значений в доверительные интервалы, границы которых вычисляют для доверительной вероятности не менее 0,95.
В случае, если гипотеза о нормальном распределении геометрического параметра не может быть принята, применяют другие методы математической статистики.
4.1-4.3 (Измененная редакция, Изм. N 1).
4.4. (Исключен, Изм. N 1).
4.5. Проверку статистической однородности технологических процессов изготовления строительных элементов, а также геометрических параметров зданий и сооружений допускается выполнять упрощенным способом в соответствии с приложением 1.
Пример проверки приведен в приложении 2.
(Измененная редакция, Изм. N 1).
4.6. Процесс считается статистически однородным по данному геометрическому параметру, если распределение действительных отклонений в объединенной выборке приближается к нормальному и характеристики точности в серии выборок, составивших объединенную выборку, стабильны во времени.
4.7. В случае, если распределение действительных отклонений не соответствует нормальному, а характеристики точности в серии выборок малого объема не стабильны, процесс не может считаться налаженным и установившимся. В этом случае следует ввести операционный контроль, установить причины нестабильности точности и произвести соответствующую настройку оборудования, после чего повторить анализ.
В любом случае, систематическая погрешность по абсолютной величине превышающая значение 1,643
, должна быть устранена регулированием.
(Измененная редакция, Изм. N 1).
5. ОЦЕНКА ТОЧНОСТИ ПРОЦЕССА
5.1. На основании результатов статистического анализа устанавливают возможность процесса обеспечивать точность параметра в соответствии с определенным классом точности по ГОСТ 21779-82.
5.2. Класс точности определяют из условия
(4)
где 
- ближайшее большее к значению 2
значение допуска для данного интервала номинального размера в соответствующих таблицах ГОСТ 21779-82;
- коэффициент, принимаемый по таблице настоящего стандарта в зависимости от значения приемочного уровня дефектности 
, принятого при контроле точности по ГОСТ 23616-79.
| 0,25 | 1,5 | 4,0 | 10,0 |
| 3,0 | 2,4 | 2,1 | 1,6 |
5.3. Для сопоставления уровня точности различных производств или в различные промежутки времени следует использовать показатель уровня точности 
, характеризующий запас точности по отношению к допуску и определяемый по формуле
(5)
где - выборочное среднеквадратичное отклонение, определяемое для статиcтически однородного процесса в случайных выборках объемом не менее 30 единиц.
5.1-5.3 (Измененная редакция, Изм. N 1).
5.4. Если по абсолютному значению оказывается меньше чем 0,14, то следует считать, что запас точности отсутствует.
Если отрицательна и по своему абсолютному значению превышает 0,14, то это означает, что процесс перешел в более низкий класс точности.
При значении , приближающемся к 0,5, следует проверить возможность отнесения процесса к более высокому классу точности.
ПРИЛОЖЕНИЕ 1 (рекомендуемое). ПОРЯДОК РАСЧЕТА статистических характеристик и проверки статистической однородности процесса упрощенным способом
ПРИЛОЖЕНИЕ 1
Рекомендуемое
1. Действительные отклонения в выборках объемом 510 единиц вносят в хронологическом порядке в табл.1.
Характеристики и вычисляют по формулам (1) и (3) настоящего стандарта.
Таблица 1
Форма таблицы для расчета характеристик 
и 
в мгновенных выборках объемом 
510
Дата измерений | |||||||||
Номер выборки | 1 | 2 | 3 | ... | ... | ||||
|
| ||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
| |||||||||
= 1
Характеристики и вычисляют по формулам (1) и (3) настоящего стандарта.
2. Действительные отклонения в каждой из выборок объема 30 единицам вносят в табл.2.
Таблица 2
Форма таблицы для расчета характеристик и 
в выборках объемом 
30
Номер |
|
|
|
| |||
1 | |||||||
|
|
| |||||
В каждой строчке вычисляют значения , 
, 
, складывают результаты вычислений по каждой графе и проверяют их правильность тождеством.
Характеристики и вычисляют по формулам (1) и (2), подставляя в них подсчитанные по табл.2 значения 
и 
.
3. Для расчета характеристик точности в объединенной выборке и проверки согласия действительного распределения с теоретическим действительные отклонения из всех выборок малого объема выписывают в порядке их возрастания, и полученное поле рассеяния между наименьшим и наибольшим отклонениями разбивают на интервалы распределения, равные цене деления измерительного инструмента, принимая целые числа за середины интервалов 
(
1, 2, 3, ..., 
- количество интервалов).
4. Подсчитывают количество отклонений, относящихся к каждому интервалу (частоты 
) и по форме табл.3 (левая часть) строят гистограмму действительных отклонений, откладывая по вертикали интервалы распределения, а по горизонтали - соответствующие им частоты.
Таблица 3
Форма таблицы для построения гистограммы и расчета характеристик и в объединенной выборке
Центры интервалов распределения | Частота отклонений в интервалах |
|
|
|
|
|
|
| ||||||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ... | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||||
| ||||||||||||||||||||
... | ||||||||||||||||||||
+1 | ||||||||||||||||||||
0 | ||||||||||||||||||||
-1 | ||||||||||||||||||||
... | ||||||||||||||||||||
| ||||||||||||||||||||
| - | - | - |
|
|
| ||||||||||||||
, мм 
При построении гистограммы следует учитывать, что отклонения конфигурации элементов всегда имеют положительный знак.
В правую часть табл.3 вносят значения 
, 
, 
, 
, 
, 
, вычисленные для каждого значения 
, принятого за середину интервала, и проверяют правильность вычислений тождеством
Значения и вычисляют по преобразованным формулам (1) и (2):
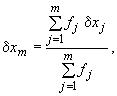(1а)
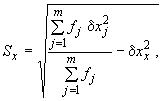(2а)
подставляя в них соответствующие суммы чисел из таблицы.
После вычисления и действительные отклонения , выходящие за пределы интервалов, в которые попадают значения 
, исключают из гистограммы и табл.3 как грубые ошибки, после чего уточняют значения и .
5. На полученной гистограмме по характеристикам и строят кривую нормального распределения. С этой целью в соответствии с табл.4 вычисляют значения 
и частоты 
, соответствующие нормальному распределению, и, отложив эти значения на вертикальной и горизонтальной шкале левой части табл.3, по полученным на гистограмме точкам с координатами и строят плавную кривую.
4
|
|
|
|
|
|
|
|
|
|
Значение 
определяют по формуле 
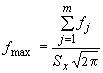, а для отклонений конфигурации - по формуле 
.
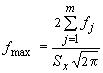6. При отсутствии на гистограмме резких отличий от построенной кривой (пиков распределения у ее границ, явно выраженных нескольких вершин и т.п.), по интервалам распределения, расположенным за пределами 
при 
2; 2,4 и 3 определяют сумму частостей действительных отклонений 
в процентах по формуле
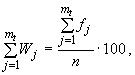
где 
- число интервалов за пределами 
.
Распределение считают приближающимся к нормальному, если найденные суммы частостей не превышают соответствующих значений, приведенных в табл.5.
5
| 2,0 | 2,4 | 3,0 |
| 12,5 | 8,6 | 5,55 |
7. Стабильность выборочного среднего отклонения и размахов в серии мгновенных выборок проверяют условиями:
где 
и 
- коэффициенты, принимаемые по табл.6 в зависимости от объема мгновенных выборок .
Таблица 6
|
|
|
5 | 1,34 | 4,89 |
6 | 1,22 | 5,04 |
7 | 1,13 | 5,16 |
8 | 1,06 | 5,25 |
9 | 1,00 | 5,34 |
10 | 0,95 | 5,43 |
При устойчивом технологическом процессе не менее 95% значений и должны соответствовать указанным условиям.
8. Стабильность характеристик и в серии выборок объемом 30 проверяют вычислением показателей 
и 
по формулам:
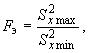
где 
и 
- соответственно наибольшее и наименьшее значения характеристики в серии выборок;
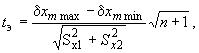
где 
и 
- соответственно наибольшее и наименьшее значения характеристики 
в серии выборок;
и 
- значения характеристики в выборках с характеристиками
и 
.
Характеристики и в серии выборок считают стабильными, если 
1,5, 
2,0.
Приложение 1. (Измененная редакция, Изм. N 1).
ПРИЛОЖЕНИЕ 2 (справочное). ПРИМЕР ПРОВЕРКИ СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
ПРИЛОЖЕНИЕ 2
Справочное
Необходимо произвести проверку статистической однородности технологического процесса изготовления панелей наружных стен. Анализируемый параметр - длина. Номинальные длины панелей всех марок находятся в интервале от 2500 до 4000 мм. Панели изготавливают в горизонтальных формах, объем выпуска - 25 панелей в смену. Парк форм для изготовления панелей - 96 шт., каждая из которых имеет свои действительные внутренние размеры, влияющие на точность соответствующих размеров панелей. Подобный технологический процесс относится к процессам серийного производства.
1. Для составления выборки объемом 30 изделий ежедневно в течение трех дней записывали действительные отклонения длины панелей, которые контролировали в соответствии с ГОСТ 11024-84 (по 5 изделий в каждую смену). Из накопленных 45 действительных отклонений были исключены пять отклонений длины изделий из форм, которые попали в контроль повторно.
Результаты измерений были округлены до целых значений в мм и внесены в табл.1, составленную по форме табл.2 приложения 1, после чего в табл.1 были выполнены необходимые вычисления.
Таблица 1
Номер п/п |
|
|
|
| |
1 | 2 | 3 | 4 | 5 | |
1 | +4 | 16 | +5 | 25 | |
2 | -3 | 9 | -2 | 4 | |
3 | -1 | 1 | 0 | 0 | |
4 | +2 | 4 | +3 | 9 | |
5 | -1 | 1 | 0 | 0 | |
6 | 0 | 0 | +1 | 1 | |
7 | -4 | 16 | -3 | 9 | |
8 | -1 | 1 | 0 | 0 | |
9 | +2 | 4 | +3 | 9 | |
10 | +1 | 1 | +2 | 4 | |
11 | +4 | 16 | +5 | 25 | |
12 | +1 | 1 | +2 | 4 | |
13 | +1 | 1 | +2 | 4 | |
14 | +3 | 9 | +4 | 16 | |
15 | +2 | 4 | +3 | 9 | |
16 | 0 | 0 | +1 | 1 | |
17 | +5 | 25 | +6 | 36 | |
18 | +3 | 9 | +4 | 16 | |
19 | +1 | 1 | +2 | 4 | |
20 | +2 | 4 | +3 | 9 | |
21 | +6 | 36 | +7 | 49 | |
22 | +2 | 4 | +3 | 9 | |
23 | +2 | 1 | +2 | 4 | |
24 | +7 | 49 | +8 | 64 | |
25 | +3 | 9 | +4 | 16 | |
26 | +2 | 4 | +3 | 9 | |
27 | +1 | 1 | +2 | 4 | |
28 | 0 | 0 | +1 | 1 | |
29 | +3 | 9 | +4 | 16 | |
30 | +2 | 4 | +3 | 9 | |
31 | 0 | 0 | +1 | 1 | |
32 | +5 | 25 | +6 | 36 | |
33 | +6 | 36 | +7 | 49 | |
34 | +2 | 4 | +3 | 9 | |
35 | +1 | 1 | +2 | 4 | |
36 | -3 | 9 | -2 | 4 | |
37 | +2 | 4 | +3 | 9 | |
38 | +3 | 9 | +4 | 16 | |
39 | +4 | 16 | +5 | 25 | |
40 | -5 | 25 | -4 | 16 | |
|
|
|
| ||
Правильность заполнения таблицы в соответствии с п.1 приложения 1 была проверена тождеством
;
после чего по формулам (1) и (2) определены
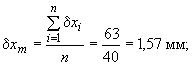
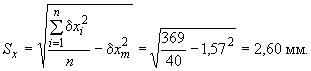
2. В течение последующих пяти месяцев в аналогичном порядке были образованы еще пять выборок того же объема 40, для каждой из которых были вычислены те же статистические характеристики и .
Сроки отбора выборок устанавливались таким образом, чтобы время между соседними выборками было больше, чем время формирования выборки.
Результаты вычислений статистических характеристик по всем выборкам приведены в табл.2.
Таблица 2
Номер п/п | Месяц, год |
|
|
|
1 | 05.78 | 40 | 1,57 | 2,60 |
2 | 06.78 | 40 | 1,43 | 2,13 |
3 | 07.78 | 40 | 0,92 | 2,22 |
4 | 08.78 | 40 | 1,05 | 2,35 |
5 | 09.78 | 40 | 1,36 | 2,18 |
6 | 10.78 | 40 | 0,87 | 2,57 |
3. Из действительных отклонений во всех выборках были выбраны наибольшее 
мм и наименьшее 
мм значения и поле рассеяния между ними разделено на 18 интервалов по 1 мм с границами, равными 10,5; 9,5; 8,5; 7,5 мм и т.д. Центры интервалов, выраженные целыми числами (
10, 9, 8, 7 мм и т.д.), были занесены в графу 2 табл.3.
Таблица 3
Гистограмма действительных отклонений и таблица расчета статистических характеристик
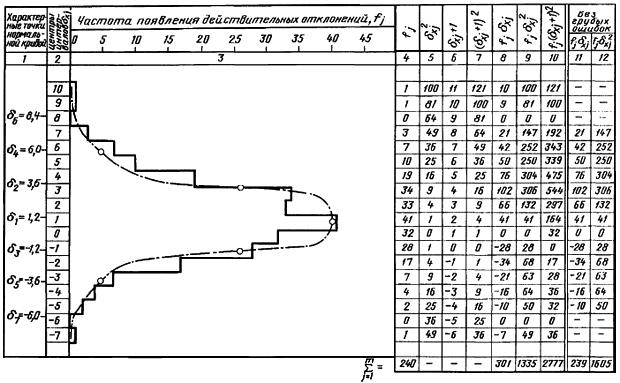
Действительные отклонения 
из всех выборок были распределены по интервалам, после чего было подсчитано количество отклонений в каждом интервале (частоты), построена гистограмма и выполнены все промежуточные вычисления в таблице. Правильность заполнения таблицы в соответствии с п.4 приложения 1 была проверена тождеством
;
Характеристики и были вычислены по формулам (1а) и (2а) приложения 1:
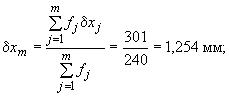
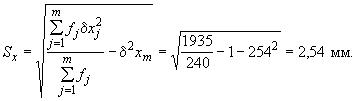
Далее вычислены значения
Отклонения, вышедшие за пределы, ограниченные вычисленными значениями и равные +10 мм, +9 мм и -7 мм, были исключены из объединенной выборки как грубые ошибки, после чего в двух последних графах табл.3 были произведены соответствующие вычисления, определены новые значения сумм 
и 
и уточнены характеристики
4. Для построения на чертеже гистограммы кривой нормального распределения в соответствии с п.4 приложения 1 были вычислены координаты точек кривой - отклонения и соответствующие им частоты .
|
|
|
|
|
|
|
|
По полученным координатам и на гистограмме были найдены характерные точки, по которым была построена теоретическая кривая нормального распределения.
Очертания гистограммы практически можно считать совпадающими с кривой нормального распределения.
Для завершения проверки по гистограмме были суммированы частоты по интервалам, расположенным за границами 
при 2,0; 2,4; 3,0, и определены соответствующие им суммы частостей.
Сравнение сумм частостей в табл.4 с допустимыми значениями в табл.5 приложения 1 показывает, что исследуемое распределение можно считать приближающимся к нормальному.
Таблица 4
Границы | Cумма частот | Сумма частостей | Допустимые суммы частостей по табл.5 |
|
|
|
|
|
|
|
|
|
|
|
|
за границами
5. Для проверки стабильности характеристики из табл.2 были выбраны наибольшее и наименьшее значения 
=2,6 мм и 
=2,13 мм и вычислена характеристика
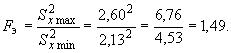
Характеристика в серии выборок стабильна, так как 
1,49 < 1,50 (см. п.8 приложения 1).
Для проверки стабильности характеристики из табл.2 были выбраны наибольшее и наименьшее значения 
=1,57 мм и 
=0,87 мм, соответствующие им значения =2,6 мм и =2,57, и вычислена характеристика
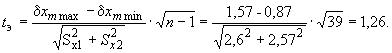
Характеристика в серии выборок стабильна, так как 
1,26 < 2 (см. п.8 приложения 1).
6. На основании проверки технологический процесс изготовления панелей наружных стен по параметру "длина панелей" можно считать статистически однородным.
Так как систематическая погрешность, равная найденному выборочному среднему отклонению 
=1,2 мм, превышает значение 
мм, то в соответствии с п.4.7 настоящего стандарта она должна быть устранена регулированием внутренних размеров форм.
7. Для определения класса точности по длине панелей, в соответствии с п.5.2 настоящего стандарта определяем значение
Значение 2,1 принято по таблице п.5.2 настоящего стандарта для приемочного уровня дефектности 
4,0%, выбранного по ГОСТ 23616-79.
В соответствии с табл.1 ГОСТ 21779-82 ближайшее большее значение допуска для интервала номинальных размеров от 2500 до 4000 мм равняется 10 мм, что соответствует 5-му классу точности.
По формуле (5) настоящего стандарта вычисляем значение
В соответствии с п.5.4 настоящего стандарта можно сделать вывод, что запас точности отсутствует, так как 0,01 < 0,14.
ПРИЛОЖЕНИЕ 2. (Измененная редакция, Изм. N 1).